Question
Question: Let A = $[a_{ij}]$ be a 3 × 3 matrix such that $a_{ij}$ = cos(iθ + jθ) for 1≤i, j ≤ 3 where θ = $\fr...
Let A = [aij] be a 3 × 3 matrix such that aij = cos(iθ + jθ) for 1≤i, j ≤ 3 where θ = 32π, then the determinant of the matrix C (where C = A + I3) is
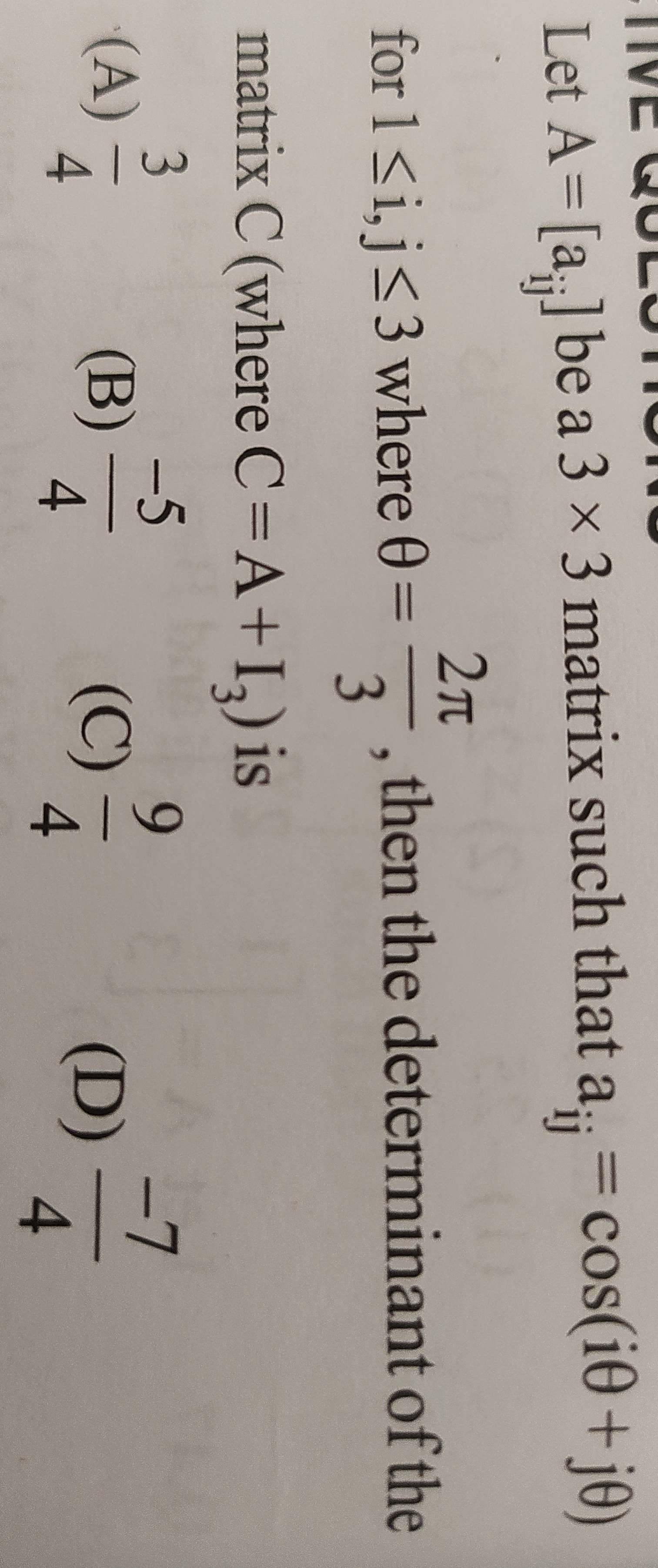
43
4−5
49
4−7
4−5
Solution
Here's how to solve this problem:
-
Construct the matrix A:
- Calculate the elements of matrix A using the formula aij=cos((i+j)θ), where θ=32π.
A=−211−211−21−21−21−211
-
Construct the matrix C:
- Add the identity matrix I3 to matrix A: C=A+I3
C=211−21121−21−21−212
-
Calculate the determinant of C:
- Use cofactor expansion along the first row to find the determinant of C.
det(C)=2121−21−212−11−21−212+(−21)1−2121−21
-
Calculate the 2x2 determinants:
-
21−21−212=(21)(2)−(−21)(−21)=1−41=43
-
1−21−212=(1)(2)−(−21)(−21)=2−41=47
-
1−2121−21=(1)(−21)−(21)(−21)=−21+41=−41
-
-
Substitute these values back into the determinant formula:
det(C)=21(43)−1(47)−21(−41)=83−47+81=83−814+81=8−10=−45
Therefore, the determinant of matrix C is −45.
