Question

Let $A{A_1}$ be the median of the triangle with vertices $A(2,2)$, $B(6, - 1)$and $C(7,3)$. The equation of line passing through and parallel $(1, - 1)$is:

Answer 1

Hint : Here the question is related to the straight line. We have to find the equation of a line. The values of the end points of the triangle are known, by considering these points we determine the midpoint of the line of the triangle. Then we can determine the equation of the line.

Complete step-by-step answer :

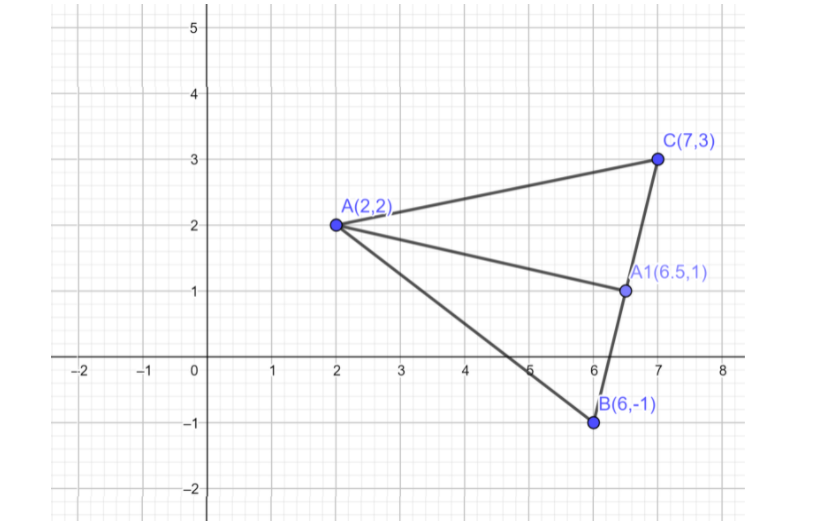
Now consider the given question.

The $A{A_1}$ is the median of the triangle, which means $A{A_1}$ is a line from a point A. The ${A_1}$ is the midpoint of the line segment BC. So by using the midpoint formula we determine the ${A_1}$.
The midpoint formula for a line is given by
midpoint = $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$, where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the endpoints of the line.
$\Rightarrow {A_1} = \left( {\dfrac{{7 + 6}}{2},\dfrac{{3 - 1}}{2}} \right)$
On simplifying we get
$\Rightarrow {A_1} = \left( {\dfrac{{13}}{2},\dfrac{2}{2}} \right)$
On further simplifying we have
$\Rightarrow {A_1} = \left( {6.5,1} \right)$
Now we determine the slope of $A{A_1}$. The formula for the slope is given by
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
The slope of $A{A_1}$= $\dfrac{{1 - 2}}{{6.5 - 2}}$
On simplifying we have
The slope of $A{A_1}$= $\dfrac{{ - 1}}{{4.5}}$
This can be written as
The slope of $A{A_1}$= $\dfrac{{ - 2}}{9}$
Now we have to determine the equation of a line which is passing through (1,-1) and parallel to $A{A_1}$
We have the formula, that is given by
$y - {y_1} = m(x - {x_1})$
The value of ${y_1} = - 1$, ${x_1} = 1$ and $m = \dfrac{{ - 2}}{9}$
On substituting these values for the formula of equation of line passing the point. Therefore we have
$\Rightarrow y - ( - 1) = \dfrac{{ - 2}}{9}(x - 1)$
$\Rightarrow y + 1 = \dfrac{{ - 2}}{9}(x - 1)$
Take 9 which is in the denominator to RHS we have
$\Rightarrow 9(y + 1) = - 2(x - 1)$
On multiplying
$\Rightarrow 9y + 9 = - 2x + 2$
Taking the terms which is present in RHS to the LHS we have
$\Rightarrow 2x + 9y + 7 = 0$
Hence we have determined the equation of a line.
So, the correct answer is “$\Rightarrow 2x + 9y + 7 = 0$”.

Note : To determine the equation of a line which is passing through the point, we have to know the formula. Students may not get confused by the word median, here median means the midline of the given triangle. Since the line is midline, there will be the midpoint for the line segment.