Question

Let A(a,0) and B(b,0) be fixed distance points on the x-axis, none of which coincides with the origin O(0,0), and let C be a point on the y-axis. Let L be a line through the O(0,0) and perpendicular to the line AC. The locus of the point of intersection of the lines L and BC if C varies along the y-axis, is (provided ${{c}^{2}}+ab\ne 0$).
(a) $\dfrac{{{x}^{2}}}{a}+\dfrac{{{y}^{2}}}{b}=x$
(b) $\dfrac{{{x}^{2}}}{a}+\dfrac{{{y}^{2}}}{b}=y$
(c) $\dfrac{{{x}^{2}}}{b}+\dfrac{{{y}^{2}}}{a}=x$
(d) $\dfrac{{{x}^{2}}}{b}+\dfrac{{{y}^{2}}}{a}=y$

Answer 1

Hint: Assume a variable point C on y axis as (0,k) and find the slope of the line AC. Using the perpendicularity condition of lines, find the slope of the line C and thus the equation of line L. Finally, substitute the expression of $k$ that you have obtained from L on the line BC for the required locus.
Given $A\left( a,0 \right)$and $B\left( b,0 \right)$ are two fixed points on x axis, let us assume the variable point C on y axis as $\left( 0,k \right)$.

Plotting the diagram with the above data, we will have it as:

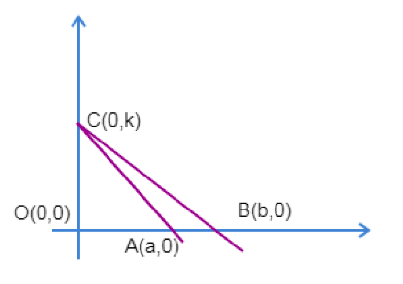
Then the slope of the line AC is given as:
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
$m=\dfrac{k-0}{0-a}$
$m=\dfrac{-k}{a}$
Now the slope of the line perpendicular to line AC is $\dfrac{-1}{m}$, since the product of slopes of perpendicular lines is -1.
Therefore, the equation of line L passing through origin and perpendicular to AC is given as:
$y=\left( \dfrac{-1}{m} \right)x$
$y=\left( \dfrac{a}{k} \right)x$
$k=\dfrac{ax}{y}$
Now the equation of line BC can be found out using $\dfrac{x}{a}+\dfrac{y}{b}=1$(intercept form) where a and b are x-intercepts and y-intercept respectively.
Therefore, the equation of line BC is:
$\dfrac{x}{a}+\dfrac{y}{k}=1$
Substituting $k=\dfrac{ax}{y}$ in the above equation we will have:
$\dfrac{x}{b}+\dfrac{y}{\left( \dfrac{ax}{y} \right)}=1$
$\dfrac{x}{b}+\dfrac{{{y}^{2}}}{ax}=1$

& \\\ & \dfrac{{{x}^{2}}}{b}+\dfrac{{{y}^{2}}}{a}=x \\\ \end{aligned}$$ Thus, the locus of point of intersection of L and BC is given as $$\dfrac{{{x}^{2}}}{b}+\dfrac{{{y}^{2}}}{a}=x$$ Hence, option A is the correct answer. Note: For any given two lines having slopes $${{m}_{1}}$$ and $${{m}_{2}}$$, then the condition for them to be parallel is $${{m}_{1}}={{m}_{2}}$$ and the condition to be perpendicular is $${{m}_{1}}.{{m}_{2}}=-1$$. Also, $$\frac{x}{a}+\frac{y}{b}=1$$, is the intercept form of a line where a and b are x-intercept and y-intercept respectively.