Question

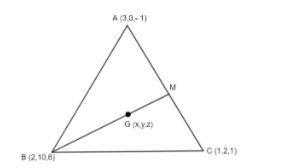
Let A (3, 0, – 1), B (2, 10, 6) and C (1, 2, 1) be the vertices of a triangle and M be the midpoint of AC. If G divides BM in the ratio, 2:1, then $\cos \left( \angle GOA \right)$ (O being the origin) is equal to:
$\left( a \right)\dfrac{1}{\sqrt{30}}$
$\left( b \right)\dfrac{1}{6\sqrt{10}}$
$\left( c \right)\dfrac{1}{\sqrt{15}}$
$\left( d \right)\dfrac{1}{2\sqrt{15}}$

Answer 1

We are given M is the midpoint of AC. So, we get the line BM is the median as G is the point on BM on dividing it into 2:1. We will get by definition of the centroid that G is the centroid then the coordinate of G is given by $x=\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},y=\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3},z=\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}.$ Then for finding cos of the angle ROA, we use $\cos \left( \angle ROA \right)=\dfrac{\left( OR \right).\left( OA \right)}{\left| OR \right|\left| OA \right|}.$ To do so we will find the magnitude of OR and OA and then find the dot product OR.OA.

Complete step-by-step answer:
We are given the coordinates of the triangle ABC as A (3, 0, – 1), B (2, 10, 6) and C (1, 2, 1). We have M as the midpoint of AC and G is the point on BM that divides BM in the ratio 2:1. We know that as M is the midpoint, so BM is the median of triangle ABC. Now, the point on the median which divides the median in 2:1 is known as the centroid.
As G lies on the median BM and divides BM in the ratio 2:1, so it means G is the centroid.

Now we know that coordinate of the centroid G is given as
$x=\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},y=\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3},z=\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}$
where $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right),\left( {{x}_{3}},{{y}_{3}},{{z}_{3}} \right)$ are the coordinates of the vertex.
As the vertex, we have A (3, 0, – 1), B (2, 10, 6), C (1, 2, 1). So, we get the coordinate of G as
$x=\dfrac{3+2+1}{3}=\dfrac{6}{3}=2$
$y=\dfrac{2+10+2}{3}=\dfrac{12}{3}=4$
$z=\dfrac{-1+6+1}{3}=\dfrac{6}{3}=2$
So, we have the coordinate as G (2, 4, 2).
Now, we have to find the cos of $\angle GOA$ where O is the origin.

We know that the cos angle between the two vectors is given as
$\cos \left( \angle XOY \right)=\dfrac{OX.OY}{\left| OX \right|\left| OY \right|}$
So, for $\angle GOA$ we will get,
$\cos \left( \angle GOA \right)=\dfrac{OG.OA}{\left| OG \right|\left| OA \right|}$
So, for G (2, 4, 2) and O (0, 0, 0) we have,
$OG=\left( 2-0 \right)i+\left( 4-0 \right)j+\left( 2-0 \right)k$
$\Rightarrow OG=2i+4j+2k$
For A (3, 0, – 1) and O (0, 0, 0), we have,
$OA=\left( 3-0 \right)i+\left( 0-0 \right)j+\left( -1-0 \right)k$
$\Rightarrow OA=3i-k$
Now,
$\left| OG \right|=\sqrt{{{2}^{2}}+{{4}^{2}}+{{2}^{2}}}$
$\Rightarrow \left| OG \right|=\sqrt{4+16+4}$
$\Rightarrow \left| OG \right|=\sqrt{24}$
And
$\left| OA \right|=\sqrt{{{3}^{2}}+{{\left( -1 \right)}^{2}}}$
$\Rightarrow \left| OA \right|=\sqrt{10}$
Also,
$OA.OG=\left( 3i-k \right)\left( 2i+4j+2k \right)$
$\Rightarrow OA.OG=6-2$
$\Rightarrow OA.OG=4$
Putting this value in $\cos \left( \angle GOA \right).$
$\cos \left( \angle GOA \right)=\dfrac{OA.OG}{\left| OA \right|\left| OG \right|}$
$\Rightarrow \cos \left( \angle GOA \right)=\dfrac{4}{\left| \sqrt{10} \right|\left| \sqrt{24} \right|}$
After simplification we get,
$\Rightarrow \cos \left( \angle GOA \right)=\dfrac{4}{2\times 2\times \sqrt{15}}$
$\Rightarrow \cos \left( \angle GOA \right)=\dfrac{1}{\sqrt{15}}$

So, the correct answer is “Option C”.

Note: To simplify the square root we need to factorize it. $\sqrt{24}$ can be written as $\sqrt{24}=\sqrt{2\times 2\times 2\times 3}$ and $\sqrt{10}=\sqrt{2\times 5}.$ So,
$\sqrt{24}\times \sqrt{10}=\sqrt{2\times 2\times 2\times 2\times 3\times 5}$
2 comes out two times as it makes a pain that gives us $2\times 2\times \sqrt{15}.$ This we use while simplifying. Also, remember that |OG| means the magnitude of OG which is given as $\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$ if OG is given as $x\widehat{i}+y\widehat{j}+2\widehat{k.}$