Solveeit Logo
Login

Question

Question: Let $(5+2\sqrt{6})^n=p+f$, where $n \in N$ and $p \in N$ and $0 < f < 1$, then the absolute value of...

Let (5+26)n=p+f(5+2\sqrt{6})^n=p+f, where n∈Nn \in N and p∈Np \in N and 0<f<10 < f < 1, then the absolute value of f2−f+pf−pf^2 - f + pf - p is __.

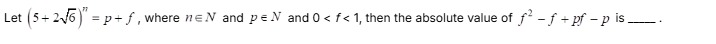
Answer

1

Explanation

Solution

Let

a=(5+26)n=p+f,b=(5−26)na = (5+2\sqrt{6})^n = p+f, \quad b = (5-2\sqrt{6})^n.

Since a+ba+b is an integer, f+b=1f+b=1 giving b=1−fb=1-f.

Then,

f2−f+pf−p=(f−1)(f+p)=−(1−f)(p+f)=−ab=−1f^2-f+pf-p = (f-1)(f+p) = -(1-f)(p+f) = -ab = -1.

So, the absolute value is 1.