Question
Question: Let $(1 + x + x^2)^{20} = \sum_{k=0}^{40} a_k x^k$. If $\alpha a_{11} = \beta a_{10} + \gamma a_9$, ...
Let (1+x+x2)20=∑k=040akxk. If αa11=βa10+γa9, where α,β,γ∈N, then the value of βγ−α is
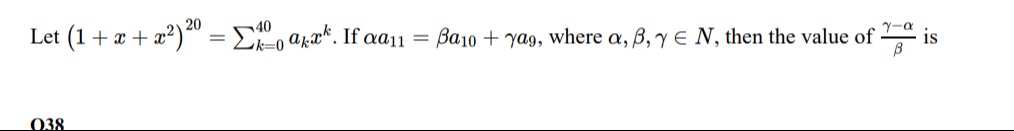
1
2
3
4
2
Solution
To find the relation between the coefficients a11,a10,a9 of the expansion (1+x+x2)20=∑k=040akxk, we use a technique involving differentiation.
Let P(x)=(1+x+x2)20.
We can write P(x)=∑k=040akxk.
Differentiate P(x) with respect to x:
P′(x)=20(1+x+x2)19(1+2x).
Now, multiply P′(x) by (1+x+x2):
P′(x)(1+x+x2)=20(1+x+x2)19(1+2x)(1+x+x2)
P′(x)(1+x+x2)=20(1+2x)(1+x+x2)20
Substitute P(x) back into the equation:
P′(x)(1+x+x2)=20(1+2x)P(x).
Now, substitute the series forms of P(x) and P′(x) into this equation:
Since P(x)=∑k=040akxk, then P′(x)=∑k=140kakxk−1.
The left-hand side (LHS) becomes:
(∑k=140kakxk−1)(1+x+x2)=∑k=140kakxk−1+∑k=140kakxk+∑k=140kakxk+1.
The right-hand side (RHS) becomes:
20(1+2x)(∑k=040akxk)=20∑k=040akxk+40∑k=040akxk+1.
Now, we equate the coefficients of x10 on both sides.
Coefficient of x10 on LHS:
From ∑k=140kakxk−1: set k−1=10⇒k=11. The term is 11a11x10.
From ∑k=140kakxk: set k=10. The term is 10a10x10.
From ∑k=140kakxk+1: set k+1=10⇒k=9. The term is 9a9x10.
So, the coefficient of x10 on LHS is 11a11+10a10+9a9.
Coefficient of x10 on RHS:
From 20∑k=040akxk: set k=10. The term is 20a10x10.
From 40∑k=040akxk+1: set k+1=10⇒k=9. The term is 40a9x10.
So, the coefficient of x10 on RHS is 20a10+40a9.
Equating the coefficients of x10:
11a11+10a10+9a9=20a10+40a9.
Rearrange the terms to match the given form αa11=βa10+γa9:
11a11=(20−10)a10+(40−9)a9
11a11=10a10+31a9.
Comparing this with αa11=βa10+γa9, we identify the values:
α=11
β=10
γ=31
Given that α,β,γ∈N, these values satisfy the condition.
Finally, we need to find the value of βγ−α:
βγ−α=1031−11=1020=2.
The final answer is 2.
Explanation of the solution:
The problem involves finding a recurrence relation between coefficients of a polynomial expansion.
- Define P(x)=(1+x+x2)20=∑k=040akxk.
- Differentiate P(x) to get P′(x)=20(1+x+x2)19(1+2x).
- Establish a relationship between P(x) and P′(x) by multiplying P′(x) by (1+x+x2):
P′(x)(1+x+x2)=20(1+2x)P(x). - Substitute the series forms of P(x) and P′(x) into this equation:
(∑k=140kakxk−1)(1+x+x2)=20(1+2x)(∑k=040akxk). - Equate the coefficients of x10 on both sides of the equation.
LHS coefficient of x10: 11a11+10a10+9a9.
RHS coefficient of x10: 20a10+40a9. - Set LHS coefficient equal to RHS coefficient: 11a11+10a10+9a9=20a10+40a9.
- Rearrange the equation to match the given form αa11=βa10+γa9:
11a11=10a10+31a9. - Identify α=11,β=10,γ=31.
- Calculate the required expression: βγ−α=1031−11=1020=2.
