Solveeit Logo
Login

Question

Question: Length of the normal chord of the parabola \({{y}^{2}}=8x\) at the point where abscissa and ordinate...

Length of the normal chord of the parabola y2=8x{{y}^{2}}=8x at the point where abscissa and ordinate are equal is:
A.13
B.8
C.10510\sqrt{5}
D.4

Explanation

Solution

Hint: Take the focal chord as PQ. Their coordinates are of the form (at2,2at)\left( a{{t}^{2}},2at \right) . From the given equation of parabola and focal chord concept, we need to get the value of a, t1{{t}_{1}} and t2{{t}_{2}} . As abscissa of ordinate are equal, y=x puts that in the equation of parabola. Get value of P & Q, using distance formula. Find length or PQ.

Complete step-by-step answer:
We have been given the equation of parabola as y2=8x{{y}^{2}}=8x .
First let us draw the parabola y2=8x{{y}^{2}}=8x

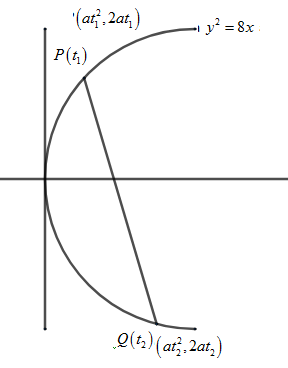
We know the general equation of a parabola as y2=4ax{{y}^{2}}=4ax , Now let us compare both the general equation and the given equation of parabola.
From that we get, latus rectum 4a=84a=8
a=84=2 i.e. a=2 \begin{aligned} & a=\dfrac{8}{4}=2 \\\ & \text{i}\text{.e}\text{. }a=2 \\\ \end{aligned}
Let us take the two points on the parabola as P(t1)P\left( {{t}_{1}} \right) and Q(t2)Q\left( {{t}_{2}} \right) . we know the relation t1t2=−1{{t}_{1}}{{t}_{2}}=-1 .
Similarly we know that t2=−t1−2t1{{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}} .
It is said that the abscissa and ordinates are equal, the coordinates are equal so put y=x.
y2=8x{{y}^{2}}=8x
So, x2=8x⇒x2−8x=0{{x}^{2}}=8x\Rightarrow {{x}^{2}}-8x=0 .
x(x−8)=0x\left( x-8 \right)=0 Hence x=0x=0 or x−8=0x-8=0
i.e. x can be either 0 or 8. So when x=8, y=8
Thus we got the coordinate of (x,y)\left( x,y \right) as (8,8)\left( 8,8 \right) .
We can take the coordinate of P(at12,2at1)P\left( at_{1}^{2},2a{{t}_{1}} \right) and Q(at22,2at2)Q\left( at_{2}^{2},2a{{t}_{2}} \right) .
Thus we got a=2, So,  P(2t12,4t1)~P\left( 2t_{1}^{2},4{{t}_{1}} \right) and Q(2t22,4at2)Q\left( 2t_{2}^{2},4a{{t}_{2}} \right) .
Now we get the coordinate of (x,y)=(8,8)\left( x,y \right)=\left( 8,8 \right) and coordinate (2t12,4t1)\left( 2t_{1}^{2},4{{t}_{1}} \right) .
Now let us equate the x and y coordinates of both.
Thus,
4t1=8 t1=84=2 \begin{aligned} & 4{{t}_{1}}=8 \\\ & {{t}_{1}}=\dfrac{8}{4}=2 \\\ \end{aligned}
Thus we got t1=2{{t}_{1}}=2
We know that t2=−t1−2t1=−2−22=−2−1=−3{{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}=-2-\dfrac{2}{2}=-2-1=-3
Thus t2=−3{{t}_{2}}=-3 .
Thus let us put t1=2{{t}_{1}}=2 and t2=−3{{t}_{2}}=-3 in the coordinate of P and Q

& ~P\left( 2t_{1}^{2},4{{t}_{1}} \right)=P\left( 2\times {{2}^{2}},4\times 2 \right)=P\left( 8,8 \right) \\\ & Q\left( 2t_{2}^{2},4a{{t}_{2}} \right)=Q\left( 2\times {{\left( -3 \right)}^{2}},4\times -3 \right)Q\left( 18,-12 \right) \\\ \end{aligned}$$ Now, let us find the length of normal chord PQ using distance formula distance$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ Put $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 8,8 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 18,12 \right)$ Length of normal chord PQ $=\sqrt{{{\left( 18-8 \right)}^{2}}+{{\left( -12-8 \right)}^{2}}}$ $$=\sqrt{{{10}^{2}}+{{\left( -20 \right)}^{2}}}=\sqrt{100+400}=\sqrt{500}=\sqrt{100\times 5}=10\sqrt{5}$$ . Hence we got the length of a normal chord as $10\sqrt{5}$ . Therefore, option (C) is the correct answer. Note: The normal at the point $$\left( 2t_{1}^{2},4{{t}_{1}} \right)$$ meets the parabola again in the point $\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ , thus ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ . We may sometimes take ${{t}_{1}}{{t}_{2}}=-1$ , but that is not concept to use and it will give us wrong values of ${{t}_{1}}$ and ${{t}_{2}}$ .