Solveeit Logo
Login

Question

Question: Length of the focal chord of the parabola \({{y}^{2}}=4ax\) at the distance p from the vertex is: ...

Length of the focal chord of the parabola y2=4ax{{y}^{2}}=4ax at the distance p from the vertex is:
A.2a3p\dfrac{2{{a}^{3}}}{p}
B.a3p2\dfrac{{{a}^{3}}}{{{p}^{2}}}
C.4a3p2\dfrac{4{{a}^{3}}}{{{p}^{2}}}
D.p2a\dfrac{{{p}^{2}}}{a}

Explanation

Solution

Hint: Take 2 points on parabola as (at12,2at1)\left( at_{1}^{2},2a{{t}_{1}} \right) and (at22,2at2)\left( at_{2}^{2},2a{{t}_{2}} \right) . use basic formula and find the length of PQ and take length of focal chord PQ as c. Now, find the equation of line PQ. Substitute the value you get in the expression of length of focal chord ‘c’ and get the value of c.

Complete step-by-step answer:
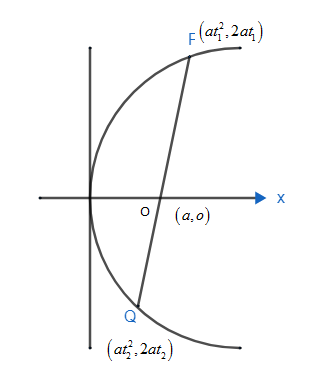
We have been given the equation of parabola as y2=4ax{{y}^{2}}=4ax . We need to find the focal chord of the parabola at a distance p from the vertex. Let us take 2 points on the parabola as P and Q. Now let us consider the coordinates as P(at12,2at1)P\left( at_{1}^{2},2a{{t}_{1}} \right) and Q(at22,2at2)Q\left( at_{2}^{2},2a{{t}_{2}} \right) . O(a,o)O\left( a,o \right) is the focus of the parabola.

We know the formula for finding slope of line as, m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} .
Here the slope of OP is equal to the slope of OQ.
i.e. t1t2=−1{{t}_{1}}{{t}_{2}}=-1 i.e. Slope of OP = Slope of OQ
⇒t2=−1t1\Rightarrow {{t}_{2}}=\dfrac{-1}{{{t}_{1}}} .
Hence in the coordinate of Q put t2=−1t1{{t}_{2}}=\dfrac{-1}{{{t}_{1}}}
∴Q(a(−1t1)2,2a(−1t1))=Q(at12,−2at1)\therefore Q\left( a{{\left( -\dfrac{1}{{{t}_{1}}} \right)}^{2}},2a\left( -\dfrac{1}{{{t}_{1}}} \right) \right)=Q\left( \dfrac{a}{t_{1}^{2}},-\dfrac{2a}{{{t}_{1}}} \right) respectively.
Let’s assume t1=−1t2=t{{t}_{1}}=\dfrac{-1}{{{t}_{2}}}=t.
Let the length of the focal chord be taken a c.
The distance of PQ can be found by using the formula, distance(x2−x1)2+(y2−y1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
Put (x2,y2)=(at2,2at)\left( {{x}_{2}},{{y}_{2}} \right)=\left( a{{t}^{2}},2at \right), (x1,y1)=(at2,−2at)\left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{a}{{{t}^{2}}},-\dfrac{2a}{t} \right).
Distance PQ=(at2−at2)2+(2at+2at)2=c=\sqrt{{{\left( a{{t}^{2}}-\dfrac{a}{{{t}^{2}}} \right)}^{2}}+{{\left( 2at+\dfrac{2a}{t} \right)}^{2}}}=c
Simplifying we get ∣PQ‾∣=a2(t2−1t2)2+(2a)2(t+1t)2=c⇒a2(t−1t)2(t+1t)2+4a2(t+1t)2=c\left| \overline{PQ} \right|=\sqrt{{{a}^{2}}{{\left( {{t}^{2}}-\dfrac{1}{{{t}^{2}}} \right)}^{2}}+{{\left( 2a \right)}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}}=c\Rightarrow \sqrt{{{a}^{2}}{{\left( t-\dfrac{1}{t} \right)}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}+4{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}}=c
We know that a2−b2=(a+b)(a−b){{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right). Similarly, (t2−1t2)2=(t−1t)2(t+1t)2{{\left( {{t}^{2}}-\dfrac{1}{{{t}^{2}}} \right)}^{2}}={{\left( t-\dfrac{1}{t} \right)}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}
\Rightarrow \left| \overline{PQ} \right|=\sqrt{{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}\left\\{ {{\left( t-\dfrac{1}{t} \right)}^{2}}+4 \right\\}}=c [taking a2(t+1t)2{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}common both the terms].
⇒a2(t+1t)2(t2+1t2−2+4)=c\Rightarrow \sqrt{{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}\left( {{t}^{2}}+\dfrac{1}{{{t}^{2}}}-2+4 \right)}=c
⇒a2(t+1t)2(t2+1t2+2)=c\Rightarrow \sqrt{{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}\left( {{t}^{2}}+\dfrac{1}{{{t}^{2}}}+2 \right)}=c we know a2+b2+2ab=(a+b)2{{a}^{2}}+{{b}^{2}}+2ab={{\left( a+b \right)}^{2}}
Similarly, a2(t+1t)2(t+1t)2=c⇒a2(t+1t)4=c\sqrt{{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{2}}}=c\Rightarrow \sqrt{{{a}^{2}}{{\left( t+\dfrac{1}{t} \right)}^{4}}}=c
Hence it become, a(t+1t)2=ca{{\left( t+\dfrac{1}{t} \right)}^{2}}=c ……………… (1)
Now, it is said that the length of the focal chord is at a distance of P from the vertex. Now, let us find the equation of PQ.
Equation of PQ can be found by using the formula, where
(x2,y2)=(at2,2at)\left( {{x}_{2}},{{y}_{2}} \right)=\left( a{{t}^{2}},2at \right), (x1,y1)=(at2,−2at)\left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{a}{{{t}^{2}}},-\dfrac{2a}{t} \right).
So, y−y1=m(x−x1)y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)
Where m = slope of line PQ =y2−y1x2−x1=2at+2atat2−at2=2a(t+1t)a(t2−1t2)=2(t+1t)(t+1t)(t−1t)=2t−1t=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{2at+\dfrac{2a}{t}}{a{{t}^{2}}-\dfrac{a}{{{t}^{2}}}}=\dfrac{2a\left( t+\dfrac{1}{t} \right)}{a\left( {{t}^{2}}-\dfrac{1}{{{t}^{2}}} \right)}=\dfrac{2\left( t+\dfrac{1}{t} \right)}{\left( t+\dfrac{1}{t} \right)\left( t-\dfrac{1}{t} \right)}=\dfrac{2}{t-\dfrac{1}{t}} .
i.e. m=2t−1tm=\dfrac{2}{t-\dfrac{1}{t}}
therefore, equation of line PQ is y+2at=2t−1t(x−at2)y+\dfrac{2a}{t}=\dfrac{2}{t-\dfrac{1}{t}}\left( x-\dfrac{a}{{{t}^{2}}} \right)
Let us simplify the expression in
⇒y+2at=2tt2−1(x−at2) ⇒(t2−1)(t2y+2at)=2t(t2x−a) ⇒(t2−1)(ty+2a)=2(t2x−a) ⇒t(t2−1)y−2t2x+a(2t2−2+2)=0 ⇒(t2−1)y−2tx+2at=0 \begin{aligned} & \Rightarrow y+\dfrac{2a}{t}=\dfrac{2t}{{{t}^{2}}-1}\left( x-\dfrac{a}{{{t}^{2}}} \right) \\\ & \Rightarrow \left( {{t}^{2}}-1 \right)\left( {{t}^{2}}y+2at \right)=2t\left( {{t}^{2}}x-a \right) \\\ & \Rightarrow \left( {{t}^{2}}-1 \right)\left( ty+2a \right)=2\left( {{t}^{2}}x-a \right) \\\ & \Rightarrow t\left( {{t}^{2}}-1 \right)y-2{{t}^{2}}x+a\left( 2{{t}^{2}}-2+2 \right)=0 \\\ & \Rightarrow \left( {{t}^{2}}-1 \right)y-2tx+2at=0 \\\ \end{aligned}
This is the equation of the focal chord.
It is said that the distance from vertex is p. we know the coordinate of vertex as (0,0)\left( 0,0 \right) .Thus by distance formula, here (x,y)=0\left( x,y \right)=0
p=∣Ax1+By1+c∣A2+B2=∣26×0−(t2−1)×0−2at∣(−2t)2+(t2−1)2=∣−2at∣4t2+(t2−1)2p=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+c \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\dfrac{\left| 26\times 0-\left( {{t}^{2}}-1 \right)\times 0-2at \right|}{\sqrt{{{\left( -2t \right)}^{2}}+{{\left( {{t}^{2}}-1 \right)}^{2}}}}=\dfrac{\left| -2at \right|}{\sqrt{4{{t}^{2}}+{{\left( {{t}^{2}}-1 \right)}^{2}}}}
Now, let us simplify this further, we know that a2−b2=(a−b)×(a+b){{a}^{2}}-{{b}^{2}}=\left( a-b \right)\times \left( a+b \right).p=∣−2at∣4t2+(t2−1)2=2at(t2+1)2=2att2+1 ⇒t2+1t=2aP ⇒t+1t=2aP \begin{aligned} & p=\dfrac{\left| -2at \right|}{\sqrt{4{{t}^{2}}+{{\left( {{t}^{2}}-1 \right)}^{2}}}}=\dfrac{2at}{\sqrt{{{\left( {{t}^{2}}+1 \right)}^{2}}}}=\dfrac{2at}{{{t}^{2}}+1} \\\ & \Rightarrow \dfrac{{{t}^{2}}+1}{t}=\dfrac{2a}{P} \\\ & \Rightarrow t+\dfrac{1}{t}=\dfrac{2a}{P} \\\ \end{aligned}
Now, substitute this in (1)
a(t+1t)2=c⇒a(2aP)2=c ⇒c=4a3P2 \begin{aligned} & a{{\left( t+\dfrac{1}{t} \right)}^{2}}=c\Rightarrow a{{\left( \dfrac{2a}{P} \right)}^{2}}=c \\\ & \Rightarrow c=\dfrac{4{{a}^{3}}}{{{P}^{2}}} \\\ \end{aligned}
Length of focal chord c=4a3P2c=\dfrac{4{{a}^{3}}}{{{P}^{2}}}. Hence, we got the required length as 4a3P2\dfrac{4{{a}^{3}}}{{{P}^{2}}}.

Note: The length of a focal chord of a parabola varies inversely as the square of the distance from its vertex. If we have length of segments of focal chords as l1{{l}_{1}} and l2{{l}_{2}} then we can find the latus rectum as 4l1l2l1+l2\dfrac{4{{l}_{1}}{{l}_{2}}}{{{l}_{1}}+{{l}_{2}}}.