Question

\left(m^{2}+m+1\right)\left(m^{2}+4 m+3\right)<0

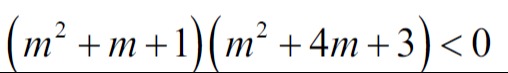
Answer 1

m \in (-3, -1)

Answer 2

The quadratic $m^2+m+1$ has a negative discriminant ($\Delta = 1^2 - 4(1)(1) = -3$) and a positive leading coefficient, so it is always positive. Thus, the inequality reduces to $m^2+4m+3 < 0$. Factoring gives $(m+1)(m+3) < 0$, which is true for $m \in (-3, -1)$.