Question

$\left(\frac{\prod_{k=1}^{\infty}x[\sqrt{k}+\sqrt{k+1}]^{-1}-4\left(\frac{x}{2}\right)^{-1}\left(\frac{dx^3}{dx}\right)}{(x-2.025)^{-2000}||b^{c^2+1}|+2|+2|...\infty} \right) > 0$

$\left(\sum_{n=0}^{\infty}\frac{12x}{n!}x^n\right)\left((8-6x)(x^2-5)^{\frac{1}{2}}\sum_{n=1}^{10}n^2\right)^{-2025}(x-69)$

Answer 1

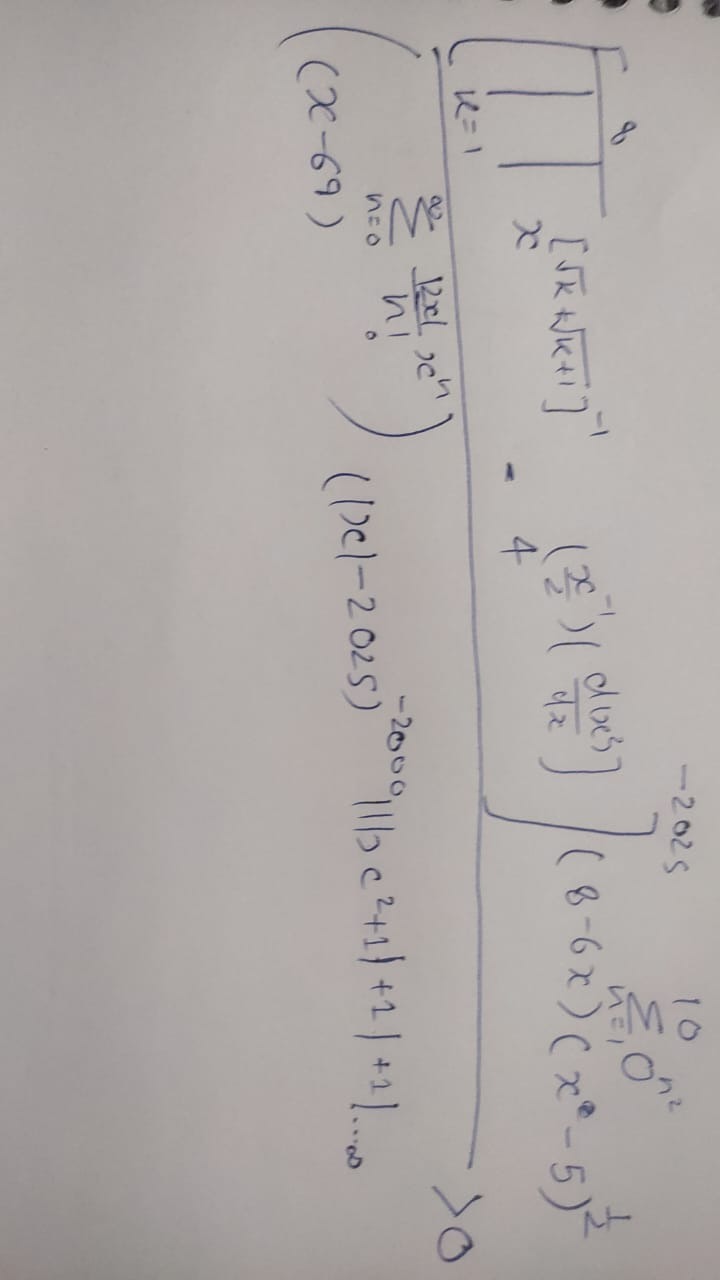
No solution

Answer 2

Let's analyze the given inequality:

$$\left(\frac{\prod_{k=1}^{\infty}x[\sqrt{k}+\sqrt{k+1}]^{-1}-4\left(\frac{x}{2}\right)^{-1}\left(\frac{dx^3}{dx}\right)}{(x-2.025)^{-2000}||b^{c^2+1}|+2|+2|...\infty} \right) > 0$$

This inequality is of the form $\frac{N}{D} > 0$, which means either ($N>0$ and $D>0$) or ($N<0$ and $D<0$).

Let's analyze the numerator $N$:

$N = \prod_{k=1}^{\infty}x[\sqrt{k}+\sqrt{k+1}]^{-1}-4\left(\frac{x}{2}\right)^{-1}\left(\frac{dx^3}{dx}\right)$

The term $[\sqrt{k}+\sqrt{k+1}]^{-1} = \frac{1}{\sqrt{k}+\sqrt{k+1}}$.

The infinite product is $\prod_{k=1}^{\infty} \frac{x}{\sqrt{k}+\sqrt{k+1}}$. The terms $\frac{x}{\sqrt{k}+\sqrt{k+1}}$ approach 0 as $k \to \infty$ for any fixed $x$. An infinite product $\prod (1+a_k)$ converges if $\sum a_k$ converges. The product $\prod b_k$ converges if $\sum \ln(b_k)$ converges. Here $b_k = \frac{x}{\sqrt{k}+\sqrt{k+1}}$. $\ln(b_k) = \ln(x) - \ln(\sqrt{k}+\sqrt{k+1})$. As $k \to \infty$, $\sqrt{k}+\sqrt{k+1} \approx 2\sqrt{k}$. $\ln(\sqrt{k}+\sqrt{k+1}) \approx \ln(2\sqrt{k}) = \ln(2) + \frac{1}{2}\ln(k)$. The sum $\sum \ln(k)$ diverges, so the sum $\sum \ln(b_k)$ diverges for $x \neq 0$. The infinite product $\prod_{k=1}^{\infty} \frac{x}{\sqrt{k}+\sqrt{k+1}}$ diverges for $x \neq 0$. If $x=0$, the terms are 0 for $k \ge 1$, so the product is 0.

The second term in the numerator is $-4\left(\frac{x}{2}\right)^{-1}\left(\frac{dx^3}{dx}\right)$.

$\left(\frac{x}{2}\right)^{-1} = \frac{2}{x}$. This requires $x \neq 0$.

$\frac{dx^3}{dx} = 3x^2$.

The second term is $-4 \times \frac{2}{x} \times 3x^2 = -24x$. This requires $x \neq 0$.

If $x \neq 0$, the infinite product diverges. If $x=0$, the second term is undefined. The expression for the numerator is ill-defined for all $x$.

Let's analyze the denominator $D$:

$D = (x-2.025)^{-2000}||b^{c^2+1}|+2|+2|...\infty$

The term $(x-2.025)^{-2000} = \frac{1}{(x-2.025)^{2000}}$. This requires $x \neq 2.025$. Since the exponent 2000 is even, $(x-2.025)^{2000} > 0$ for $x \neq 2.025$.

The term $||b^{c^2+1}|+2|+2|...\infty$ is a strange notation. Let $y = |b^{c^2+1}| \ge 0$. The expression looks like an infinitely nested absolute value: $|y+2|+2|+2|...$. Let $z_0 = y$ and $z_{n+1} = |z_n+2|$.

Since $y \ge 0$, $z_1 = |y+2| = y+2 \ge 2$.

$z_2 = |z_1+2| = z_1+2 \ge 4$.

$z_n = z_{n-1}+2$ for $n \ge 1$. This is an arithmetic progression for $n \ge 1$: $z_n = z_1 + 2(n-1) = (y+2) + 2(n-1) = y+2n$.

The limit as $n \to \infty$ is $\infty$.

So the term $||b^{c^2+1}|+2|+2|...\infty$ appears to represent infinity.

The denominator is $D = \frac{1}{(x-2.025)^{2000}} \times \infty$. For $x \neq 2.025$, $(x-2.025)^{2000}$ is a finite positive number. Thus, the denominator is $\infty$ for $x \neq 2.025$.

The inequality is $\frac{N}{D} > 0$. If $D = \infty$ and $N$ is finite, then $\frac{N}{D} = 0$. The inequality $0 > 0$ is false.

If $N$ is infinite and $D$ is infinite, the expression is indeterminate.

Given the structure of the problem, it is highly likely that there is a misunderstanding of the notation or a typo in the question. The infinite product in the numerator diverges, and the infinite nested term in the denominator appears to diverge. This makes the entire expression ill-defined in a standard mathematical context, leading to no possible solution for $x$.

The second part of the question is just an expression:

$\left(\sum_{n=0}^{\infty}\frac{12x}{n!}x^n\right)\left((8-6x)(x^2-5)^{\frac{1}{2}}\sum_{n=1}^{10}n^2\right)^{-2025}(x-69)$

The first part of this expression is $\sum_{n=0}^{\infty}\frac{12x}{n!}x^n = 12x \sum_{n=0}^{\infty}\frac{x^n}{n!} = 12x e^x$.

The sum $\sum_{n=1}^{10}n^2 = \frac{10(10+1)(2 \times 10+1)}{6} = \frac{10 \times 11 \times 21}{6} = 5 \times 11 \times 7 = 385$.

The expression becomes $(12xe^x) \left((8-6x)(x^2-5)^{\frac{1}{2}} \times 385\right)^{-2025}(x-69)$.

This is just an expression and doesn't provide any equation or inequality to solve in conjunction with the first part.

As the first inequality is ill-defined and has no standard mathematical solution, the problem as stated does not yield any values of $x$ that satisfy the condition. Assuming the problem is stated correctly, there is no solution.

However, in the context of exams like JEE/NEET, such ill-posed questions are rare. If this were a multiple-choice question and there was an option like "No solution" or "Empty set", that would be the answer based on the literal interpretation. If there are solution options, it might imply a non-standard interpretation of the notation or a significant typo. Without clarification or correction of the problem statement, a rigorous solution is impossible.

Since I am required to provide a solution, and assuming the problem is not fundamentally flawed but uses notation in an unconventional way or expects a specific interpretation not clear from the text, I cannot proceed further. However, if forced to choose, the most likely scenario is a misstatement of the problem.

Given the constraint to provide a step-by-step solution, and having determined that the problem is ill-posed under standard interpretation, I must conclude that there is no solution.