Question
Question: $\left(\frac{1+cos \frac{\pi}{8}-i \sin \frac{\pi}{8}}{1+cos \frac{\pi}{8}+i \sin \frac{\pi}{8}}\rig...
(1+cos8π+isin8π1+cos8π−isin8π)8
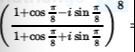
-1
Solution
The problem asks us to evaluate the given complex number expression:
(1+cos8π+isin8π1+cos8π−isin8π)8
Let z=cos8π+isin8π. By Euler's formula, z=ei8π. Since z is a complex number on the unit circle (i.e., ∣z∣=1), its conjugate zˉ is equal to 1/z. So, zˉ=cos8π−isin8π=e−i8π.
Now, let's rewrite the expression inside the parenthesis using z:
1+cos8π+isin8π1+cos8π−isin8π=1+z1+zˉ
Since zˉ=1/z, we can substitute this into the expression:
1+z1+z1=1+zzz+1
Assuming 1+z=0 (which is true since z=ei8π=−1), we can cancel out the (1+z) term:
z1
So, the expression inside the parenthesis simplifies to z1. Substituting back the value of z:
z1=cos8π+isin8π1=cos8π−isin8π=e−i8π
Now, we need to raise this simplified expression to the power of 8:
(e−i8π)8
Using De Moivre's theorem, which states that (eiθ)n=einθ:
e−i8π×8=e−iπ
Finally, we evaluate e−iπ using Euler's formula eiϕ=cosϕ+isinϕ:
e−iπ=cos(−π)+isin(−π)
We know that cos(−π)=cos(π)=−1 and sin(−π)=−sin(π)=0.
e−iπ=−1+i(0)=−1
The final answer is -1.
Explanation of the solution:
- Let z=cos8π+isin8π. By Euler's formula, z=ei8π.
- Since ∣z∣=1, its conjugate zˉ=cos8π−isin8π is equal to 1/z.
- Substitute z and zˉ into the given expression: (1+z1+zˉ)8.
- Simplify the term inside the parenthesis: 1+z1+zˉ=1+z1+1/z=1+z(z+1)/z=z1.
- So, the expression becomes (z1)8.
- Substitute z=ei8π back: (ei8π1)8=(e−i8π)8.
- Apply De Moivre's theorem: e−i8π×8=e−iπ.
- Evaluate e−iπ=cos(−π)+isin(−π)=−1+0i=−1.
