Question

$\left| {x - 1} \right| + \left| {x + 2} \right| \geqslant 3$ , then the complete solution set of this inequality is?
(The question has multiple correct options.)
A) $[1,\infty )$
B) $( - \infty , - 2]$
C) $R$
D) $[ - 2,1]$

Answer 1

Separate an inequality into two inequalities before attempting to solve it. Many basic inequalities may be overcome by inserting or subtracting all sides before the element is all that remains. Then we decide if the solution should be a fixed union ("or") or a set intersection ("and").

Complete step by step solution:
The absolute value or modulus of a real number $x$, denoted $\left| x \right|$ , is the non-negative value of $x$ regardless of its symbol. In other words, if $x$ is positive, $\left| x \right| = x$ , and if $x$ is negative (in which case $- x$ is positive), $\left| x \right| = - x$ .
Hence, there are two cases :
Case 1 : when it is positive
$\Rightarrow x - 1 + x + 2 \geqslant 3 \\\ \Rightarrow 2x + 1 \geqslant 3 \\\ \Rightarrow 2x \geqslant 3 - 1 \\\ \Rightarrow 2x \geqslant 2 \\\ \Rightarrow x \geqslant 1 \\\$
Now, since $x \geqslant 1$ , we get $x \in [1,\infty )$
Case 2: When it is negative
$\Rightarrow x - 1 + x + 2 \leqslant - 3 \\\ \Rightarrow 2x + 1 \leqslant - 3 \\\ \Rightarrow 2x \leqslant - 4 \\\ \Rightarrow x \leqslant - 2 \\\$
Now, since $x \leqslant - 2$, we get $x \in ( - \infty , - 2]$
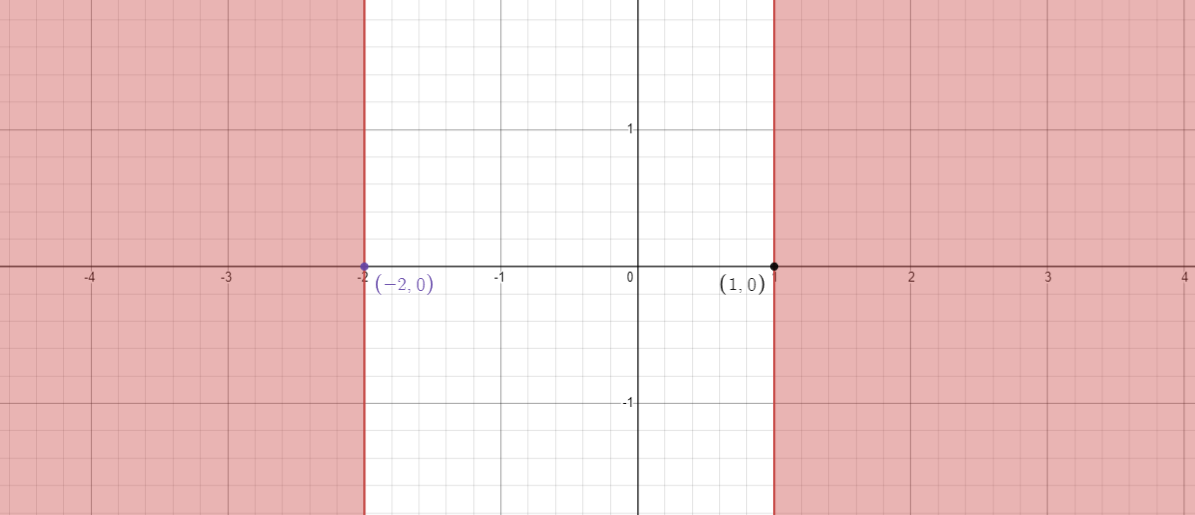
When we combine the above two cases we get, $x \in ( - \infty , - 2] \cup [1,\infty )$
Hence, the correct options are A) $[1,\infty )$ and B) $( - \infty , - 2]$.
The graph of the region (red color) is shown in the below figure.

Note:
If the absolute value expression equals a negative number, the equation has no solution since an absolute value can never be negative. An absolute value inequality can be expressed as a compound inequality.