Question
Question: $\left[-\frac{1}{Sinh^{2}a} + \frac{1}{Sinh^{4}a} - \frac{1}{2} \right]$...
[−Sinh2a1+Sinh4a1−21]
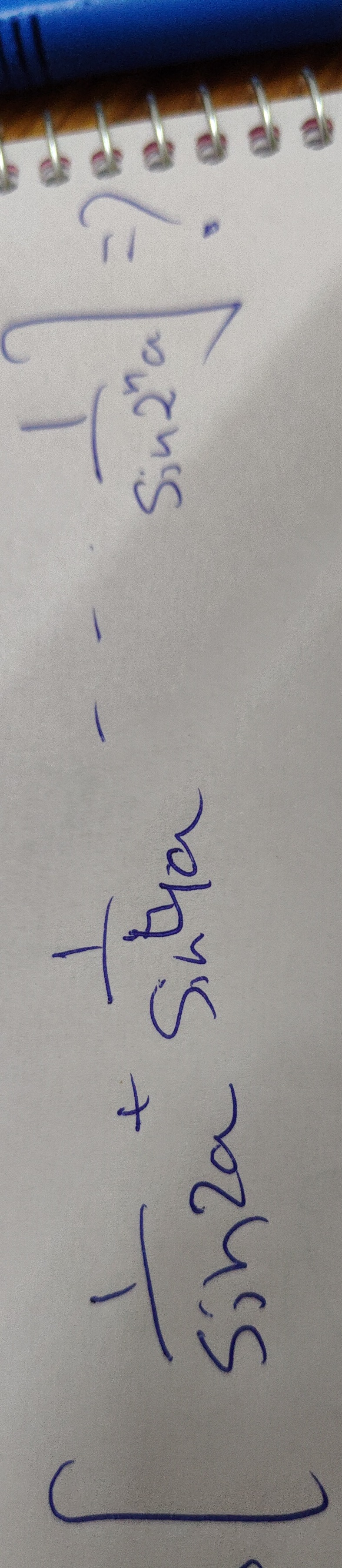
Answer
Coth4a−3Coth2a+23
Explanation
Solution
To simplify the given expression [−Sinh2a1+Sinh4a1−21], we can use the fundamental hyperbolic identity.
The identity we will use is: Coth2a−Cosech2a=1
Since Cosech2a=Sinh2a1, we can write: Coth2a−Sinh2a1=1
From this, we can express Sinh2a1 in terms of Coth2a: Sinh2a1=Coth2a−1
Let's substitute x=Sinh2a1 into the given expression. The expression becomes: x2−x−21
Now, substitute x=Coth2a−1 into this quadratic expression: (Coth2a−1)2−(Coth2a−1)−21
Expand the terms: =(Coth4a−2Coth2a+1)−(Coth2a−1)−21 =Coth4a−2Coth2a+1−Coth2a+1−21
Combine like terms: =Coth4a−(2Coth2a+Coth2a)+(1+1−21) =Coth4a−3Coth2a+(2−21) =Coth4a−3Coth2a+24−1 =Coth4a−3Coth2a+23
This is the simplified form of the expression.
