Question
Question: $( \lbrack 0,1\rbrack \ni x: \frac{x}{1} + x = (x)f(w)$...
([0,1]∋x:1x+x=(x)f(w)
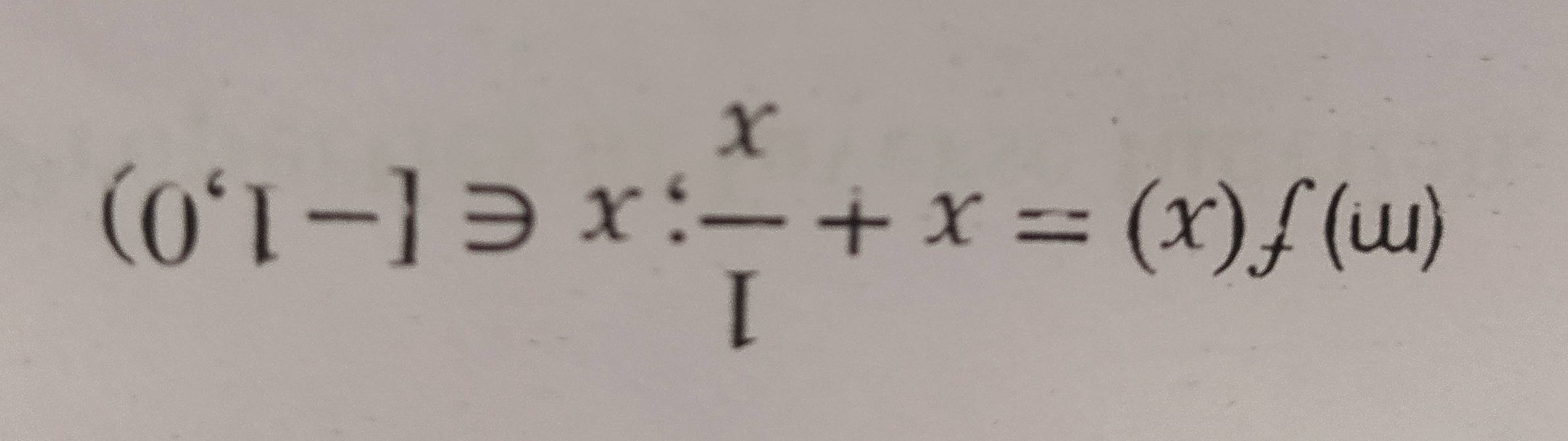
f(w)=2
Solution
The given equation is 1x+x=(x)f(w) for x∈[0,1]. The left side simplifies to x+x=2x. So the equation is 2x=(x)f(w) for all x∈[0,1].
Let's consider the standard interpretation of juxtaposition in algebra, where (x)f(w) means x×f(w). In this case, the equation is 2x=xf(w) for all x∈[0,1].
We can rearrange the equation as 2x−xf(w)=0, which is x(2−f(w))=0. This equation must hold for all x∈[0,1].
For this product to be zero for all x∈[0,1], either x=0 or 2−f(w)=0. If we choose any value of x in the interval (0,1] (i.e., x=0), the equation x(2−f(w))=0 implies that 2−f(w) must be zero.
2−f(w)=0
f(w)=2.
This means that f(w) must be equal to 2. Let's check if f(w)=2 satisfies the equation for all x∈[0,1]. Substitute f(w)=2 into the equation x(2−f(w))=0:
x(2−2)=0
x(0)=0
0=0.
This equation is true for all values of x. Since it holds for all x∈[0,1], the value f(w)=2 is the solution.
Solving 2x=xf(w) for f(w) for all x∈[0,1]:
For x∈(0,1], we can divide by x, giving f(w)=2.
For x=0, the equation becomes 2(0)=0⋅f(w), which is 0=0⋅f(w), or 0=0. This equation is satisfied for any value of f(w).
However, since the equation must hold for all x∈[0,1], the value of f(w) must be the same constant that works for all x. The value f(w)=2 works for x∈(0,1] and also works for x=0.
Thus, the only value of f(w) that satisfies the equation for all x∈[0,1] is f(w)=2.
