Question
Question: $\Lambda_m$ for 0.01 M nicotinic acid (weak monoprotic acid) is 10 times smaller than that of 0.1 M ...
Λm for 0.01 M nicotinic acid (weak monoprotic acid) is 10 times smaller than that of 0.1 M formic acid. If
λnicotinateion∘=λformateion∘ then, (α<<1 for both acids)
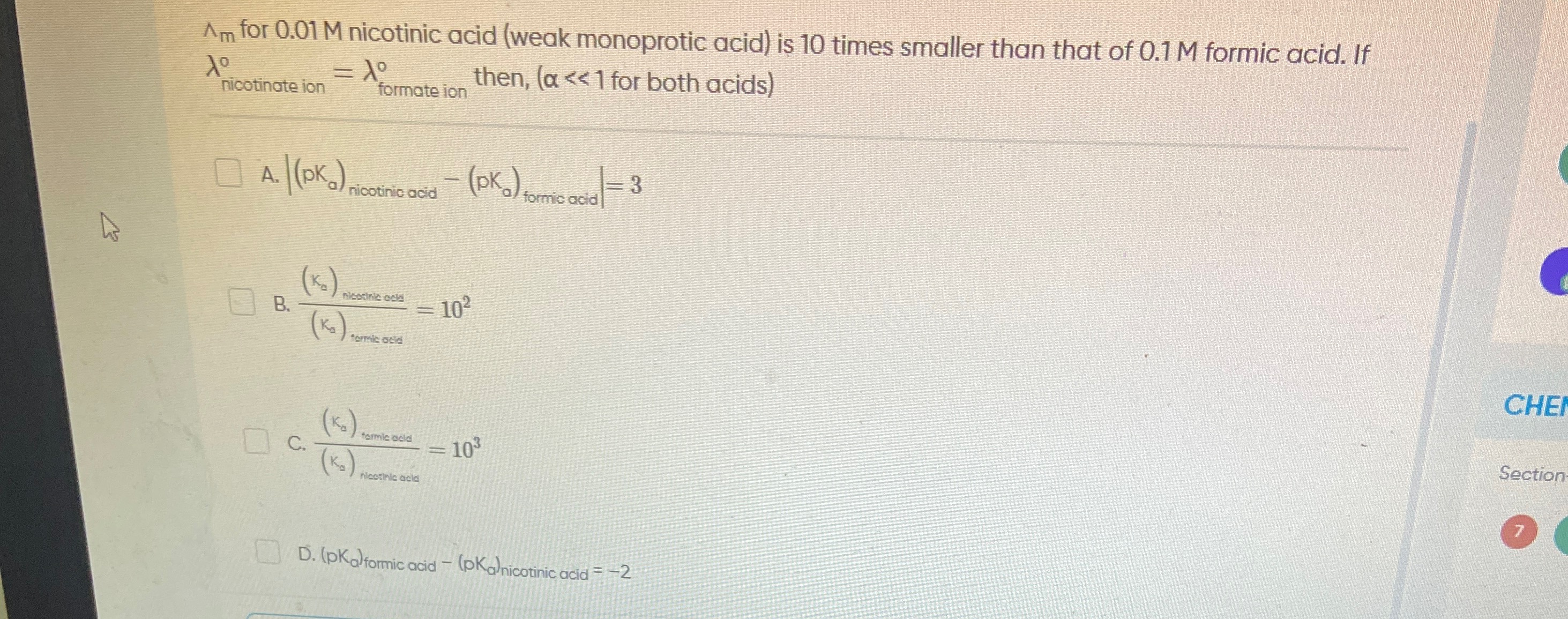
∣(pKa)nicotinic acid−(pKa)formic acid∣=3
(Ka)formic acid(Ka)nicotinic acid=102
(Ka)nicotinic acid(Ka)formic acid=103
(pKa)formic acid−(pKa)nicotinic acid=−2
A, C
Solution
The problem involves comparing the dissociation constants (Ka) and pKa values of two weak monoprotic acids: nicotinic acid (HA1) and formic acid (HA2), based on their molar conductivities.
1. Given Information and Relationships:
-
Nicotinic Acid (HA1):
- Concentration, C1=0.01 M
- Molar conductivity, Λm1
- Degree of dissociation, α1
- Dissociation constant, (Ka)1
-
Formic Acid (HA2):
- Concentration, C2=0.1 M
- Molar conductivity, Λm2
- Degree of dissociation, α2
- Dissociation constant, (Ka)2
-
Conductivity Relationship: Λm1=101Λm2
-
Limiting Molar Conductivity of Ions: λnicotinateion∘=λformateion∘
-
Approximation: α<<1 for both acids.
2. Limiting Molar Conductivities of Acids (Λm∘):
For a monoprotic acid HA, Λm∘=λH+∘+λA−∘.
- For nicotinic acid: Λm1∘=λH+∘+λnicotinateion∘
- For formic acid: Λm2∘=λH+∘+λformateion∘
Since λnicotinateion∘=λformateion∘, it implies that Λm1∘=Λm2∘. Let's denote this common value as Λ∘.
3. Relation between Molar Conductivity and Degree of Dissociation:
The degree of dissociation (α) for a weak electrolyte is given by α=Λm∘Λm. So, Λm=αΛm∘.
- For nicotinic acid: Λm1=α1Λ∘
- For formic acid: Λm2=α2Λ∘
4. Using the Given Conductivity Relationship:
Substitute the expressions for Λm1 and Λm2 into the given relation Λm1=101Λm2: α1Λ∘=101(α2Λ∘) Since Λ∘=0, we can cancel it out: α1=101α2⟹α2=10α1
5. Relation between Degree of Dissociation and Dissociation Constant (Ka):
For a weak acid HA, HA⇌H++A−.
At equilibrium, concentrations are C(1−α), Cα, Cα. The dissociation constant is Ka=[HA][H+][A−]=C(1−α)(Cα)(Cα)=1−αCα2. Given that α<<1, we can approximate 1−α≈1. So, Ka=Cα2. This implies α=CKa.
6. Applying to Both Acids:
- For nicotinic acid: (Ka)1=C1α12=0.01α12
- For formic acid: (Ka)2=C2α22=0.1α22
7. Substituting α2=10α1 into the Ka expression for formic acid:
(Ka)2=0.1(10α1)2=0.1(100α12)=10α12
8. Finding the Ratio of Ka Values:
Now, let's find the ratio of the dissociation constants: (Ka)1(Ka)2=0.01α1210α12=0.0110=1/10010=10×100=1000 So, (Ka)nicotinic acid(Ka)formic acid=103. This matches option C.
9. Finding the Relationship between pKa Values:
We know that pKa=−logKa. From (Ka)nicotinic acid(Ka)formic acid=103: Take logarithm on both sides: log((Ka)nicotinic acid(Ka)formic acid)=log(103) log(Ka)formic acid−log(Ka)nicotinic acid=3 Multiply by -1: −(log(Ka)formic acid−log(Ka)nicotinic acid)=−3 (−log(Ka)formic acid)−(−log(Ka)nicotinic acid)=−3 (pKa)formic acid−(pKa)nicotinic acid=−3
Now, let's check the options:
- A. ∣(pKa)nicotinic acid−(pKa)formic acid∣=3 From our result, (pKa)nicotinic acid−(pKa)formic acid=3. So, ∣(pKa)nicotinic acid−(pKa)formic acid∣=∣3∣=3. This option is correct.
- B. (Ka)formic acid(Ka)nicotinic acid=102 From our result, (Ka)formic acid(Ka)nicotinic acid=1031=10−3. This option is incorrect.
- C. (Ka)nicotinic acid(Ka)formic acid=103 This matches our derived result. This option is correct.
- D. (pKa)formic acid−(pKa)nicotinic acid=−2 From our result, (pKa)formic acid−(pKa)nicotinic acid=−3. This option is incorrect.
Both options A and C are correct based on the calculations.
The final answer is A,C
Explanation of the solution:
- Equate limiting molar conductivities: Since the limiting molar conductivities of the anions are equal (λnicotinateion∘=λformateion∘) and both acids share the λH+∘ component, their limiting molar conductivities (Λm∘) are equal.
- Relate Λm and α: Use the formula Λm=αΛm∘. Given Λm,nic=101Λm,form and Λm,nic∘=Λm,form∘, it leads to αnic=101αform, or αform=10αnic.
- Relate Ka and α: For weak acids with α<<1, Ka=Cα2.
- Calculate Ka ratio: Substitute the concentrations (Cnic=0.01 M, Cform=0.1 M) and the relationship between α values into the Ka expressions. (Ka)nic=0.01αnic2 (Ka)form=0.1αform2=0.1(10αnic)2=0.1(100αnic2)=10αnic2 The ratio (Ka)nic(Ka)form=0.01αnic210αnic2=0.0110=1000=103. This confirms option C.
- Calculate pKa difference: Use the relation pKa=−logKa. From (Ka)nic(Ka)form=103, taking negative logarithm yields (pKa)form−(pKa)nic=−3. Therefore, (pKa)nic−(pKa)form=3. So, ∣(pKa)nic−(pKa)form∣=∣3∣=3. This confirms option A.
