Question

$\L_2 = \lim_{x\to\infty} \int_0^x \frac{(1+\cos t)^2}{x}dt$

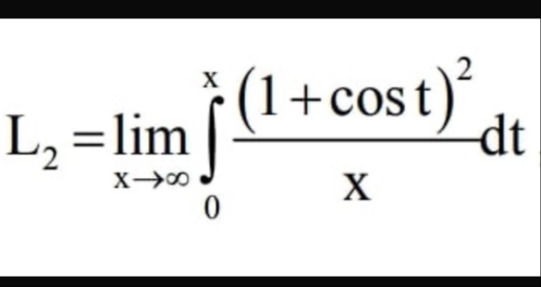
Answer 1

3/2

Answer 2

We need to evaluate:

$$L_2 = \lim_{x\to\infty}\frac{1}{x}\int_0^x (1+\cos t)^2\,dt.$$

1. Expand the integrand:

   $$(1+\cos t)^2 = 1 + 2\cos t + \cos^2 t.$$

2. Use the identity for $\cos^2 t$:

   $$\cos^2 t = \frac{1+\cos 2t}{2}.$$

   So,

   $$(1+\cos t)^2 = 1 + 2\cos t + \frac{1+\cos 2t}{2} = \frac{3}{2} + 2\cos t + \frac{1}{2}\cos2t.$$

3. Integrate term by term:

   $$\int_0^x \frac{3}{2}\,dt = \frac{3}{2}x,$$ $$\int_0^x 2\cos t\,dt = 2\sin t\Big|_0^x = 2\sin x,$$ $$\int_0^x \frac{1}{2}\cos2t\,dt = \frac{1}{2}\cdot\frac{1}{2}\sin2t\Big|_0^x = \frac{1}{4}\sin2x.$$

4. Combine the results:

   $$\int_0^x (1+\cos t)^2\,dt = \frac{3}{2}x + 2\sin x + \frac{1}{4}\sin2x.$$

5. Divide by $x$ and take the limit:

   $$L_2 = \lim_{x\to\infty} \left(\frac{3}{2} + \frac{2\sin x}{x} + \frac{\sin2x}{4x}\right).$$

   As $x\to\infty$, the terms $\frac{2\sin x}{x}$ and $\frac{\sin2x}{4x}$ approach 0. Thus,

   $$L_2 = \frac{3}{2}.$$

Core Explanation:

• Expand $(1+\cos t)^2$ and simplify.
• Integrate each term and divide by $x$.
• In the limit, oscillatory sine terms vanish.