Question
Question: $\qquad L = \lim_{x \to 0} \frac{2(\csc x - n \cot 2x)}{x^3(\cot x \csc x - \sec x)}$ = some integer...
L=limx→0x3(cotxcscx−secx)2(cscx−ncot2x) = some integer and n∈I, then the value of n+L is ____.
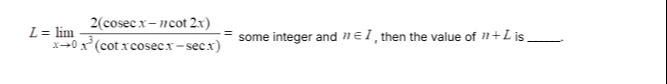
5
Solution
To evaluate the limit L=limx→0x3(cotxcscx−secx)2(cscx−ncot2x), we first simplify the expression by converting trigonometric functions into sinx and cosx.
Step 1: Simplify the numerator
Numerator N(x)=2(cscx−ncot2x)
N(x)=2(sinx1−nsin2xcos2x)
Using sin2x=2sinxcosx:
N(x)=2(sinx1−n2sinxcosxcos2x)
N(x)=sinx2(1−2cosxncos2x)
N(x)=sinx2(2cosx2cosx−ncos2x)
N(x)=sinxcosx2cosx−ncos2x
Step 2: Simplify the denominator
Denominator D(x)=x3(cotxcscx−secx)
D(x)=x3(sinxcosx⋅sinx1−cosx1)
D(x)=x3(sin2xcosx−cosx1)
D(x)=x3(sin2xcosxcos2x−sin2x)
Using cos2x−sin2x=cos2x:
D(x)=x3(sin2xcosxcos2x)
Step 3: Substitute simplified expressions into the limit
L=limx→0x3(sin2xcosxcos2x)sinxcosx2cosx−ncos2x
L=limx→0sinxcosx2cosx−ncos2x⋅x3cos2xsin2xcosx
L=limx→0x3cos2x(2cosx−ncos2x)sinx
We can rewrite this as:
L=limx→0x22cosx−ncos2x⋅xsinx⋅cos2x1
Step 4: Evaluate the limit using standard limit forms
As x→0, we know:
limx→0xsinx=1
limx→0cos2x=cos0=1
So, the limit simplifies to:
L=limx→0x22cosx−ncos2x⋅1⋅1
L=limx→0x22cosx−ncos2x
Step 5: Determine the value of n
For the limit to be finite (as L is an integer), the numerator must approach 0 as x→0 (since the denominator approaches 0).
Let f(x)=2cosx−ncos2x.
f(0)=2cos0−ncos0=2(1)−n(1)=2−n.
For the limit to be of the form 00, we must have 2−n=0, which implies n=2.
Step 6: Calculate the value of L using n=2
Substitute n=2 into the limit expression:
L=limx→0x22cosx−2cos2x
This is of the form 00, so we can apply L'Hopital's Rule.
Differentiate the numerator and denominator with respect to x:
dxd(2cosx−2cos2x)=−2sinx−2(−sin2x)(2)=−2sinx+4sin2x
dxd(x2)=2x
So, L=limx→02x−2sinx+4sin2x
L=limx→0(2x−2sinx+2x4sin2x)
L=limx→0(−xsinx+2xsin2x)
To use the standard limit limy→0ysiny=1, we adjust the second term:
L=limx→0(−xsinx+42xsin2x)
L=−(1)+4(1)
L=−1+4=3.
Alternatively, using Taylor series expansion:
cosx=1−2!x2+O(x4)
cos2x=1−2!(2x)2+O(x4)=1−2x2+O(x4)
Numerator =2cosx−2cos2x=2(1−2x2)−2(1−2x2)+O(x4)
=(2−x2)−(2−4x2)+O(x4)
=3x2+O(x4)
L=limx→0x23x2+O(x4)=limx→0(3+O(x2))=3.
Step 7: Calculate n+L
We found n=2 and L=3.
n+L=2+3=5.
The final answer is 5.
