Question

On a particular day rain drops are falling vertically at a speed of 5 m/s. A man holding a plastic board is running to escape from rain as shown. The lower end of board is at a height half that of man and the board makes 45° with horizontal. The maximum speed of man so that his feet does not get wet, is

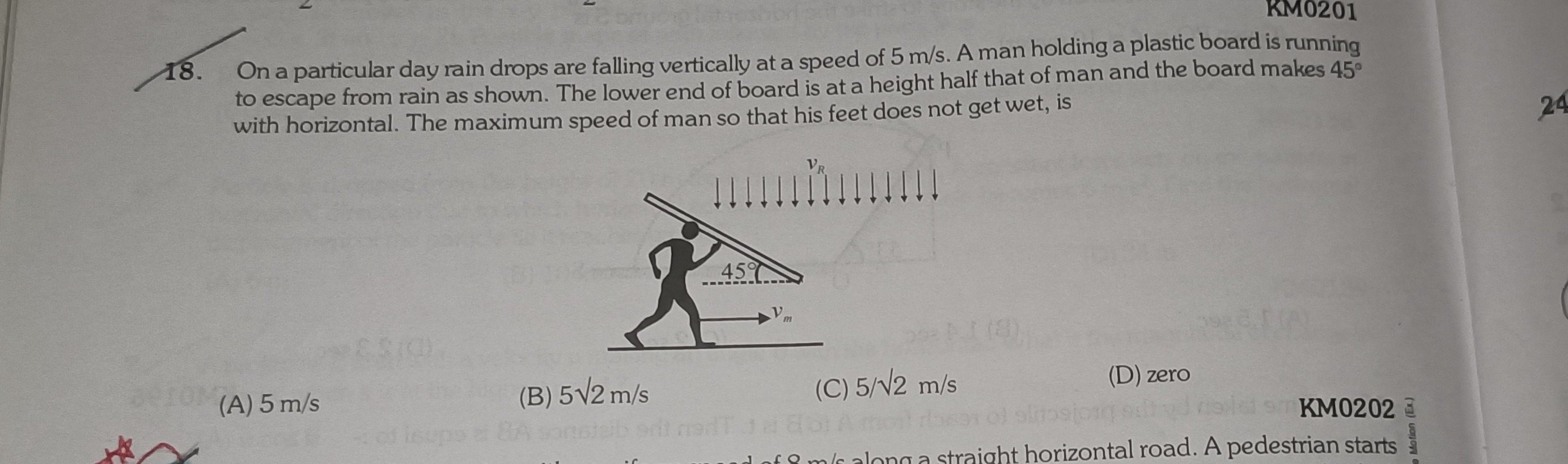
• A. 5 m/s
• B. 5√2 m/s
• C. 5/√2 m/s
• D. zero

Answer 1

Answer: (A)

5 m/s

Answer 2

Let $v_R$ be the speed of rain and $v_M$ be the speed of the man. The velocity of rain relative to the man is $\vec{v}_{R/M} = \vec{v}_R - \vec{v}_M$. With $\vec{v}_R = -v_R \hat{j}$ and $\vec{v}_M = v_M \hat{i}$, we have $\vec{v}_{R/M} = -v_M \hat{i} - v_R \hat{j}$. The angle $\phi$ that $\vec{v}_{R/M}$ makes with the downward vertical is given by $\tan \phi = \frac{|-v_M|}{|-v_R|} = \frac{v_M}{v_R}$. The board is at 45° with the horizontal, tilted upwards, so it is at 45° with the vertical, tilted forward. For the feet not to get wet, the relative velocity of the rain should be blocked by the board. This happens if the angle $\phi$ is less than or equal to the angle of the board with the vertical, which is 45°. So, $\phi \le 45^\circ$. This implies $\tan \phi \le \tan 45^\circ$, so $\frac{v_M}{v_R} \le 1$, or $v_M \le v_R$. The maximum speed of the man is when $v_M = v_R$. Given $v_R = 5$ m/s, the maximum speed of the man is 5 m/s.