Question

Solve the equation $k[k-2]+3k(5+k)+1[10+k^2]=\pm56$ for $k$.

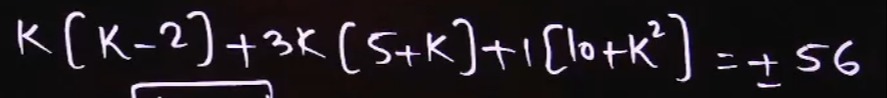
Answer 1

The real values of $k$ are $2$ and $-\frac{23}{5}$.

Answer 2

Expand and simplify the equation: $k^2 - 2k + 15k + 3k^2 + 10 + k^2 = \pm56$ $5k^2 + 13k + 10 = \pm56$

This leads to two separate equations:

Case 1: $5k^2 + 13k + 10 = 56$ $5k^2 + 13k - 46 = 0$ Using the quadratic formula, $k = \frac{-13 \pm \sqrt{13^2 - 4(5)(-46)}}{2(5)} = \frac{-13 \pm \sqrt{169 + 920}}{10} = \frac{-13 \pm \sqrt{1089}}{10} = \frac{-13 \pm 33}{10}$ $k_1 = \frac{-13 + 33}{10} = \frac{20}{10} = 2$ $k_2 = \frac{-13 - 33}{10} = \frac{-46}{10} = -\frac{23}{5}$

Case 2: $5k^2 + 13k + 10 = -56$ $5k^2 + 13k + 66 = 0$ The discriminant is $\Delta = 13^2 - 4(5)(66) = 169 - 1320 = -1151$. Since $\Delta < 0$, there are no real solutions in this case.

The real solutions are $k=2$ and $k=-\frac{23}{5}$.