Question

Kirchoff's law of of junctions is also called the law of conservation of:
(A) Energy
(B) Charge
(C) Momentum
(D) Angular Momentum

Answer 1

Hint Kirchoff's law of junctions tells us about the distribution of current in a circuit. It states that at a junction of a circuit (which is a place where several wires are joined), total ingoing current on that junction from one side should be equal to total outgoing current to the other side.

Complete step by step answer:

Current in a circuit is due to flow of charge along the wire in the circuit. Since, Kirchoff’s law states that total current coming from one side in the junction is equal to total outgoing current to other sides of the junction.

Since, rate of flow of charge is current, therefore, total charge coming to the junction should be equal to the outgoing charge from the junction.

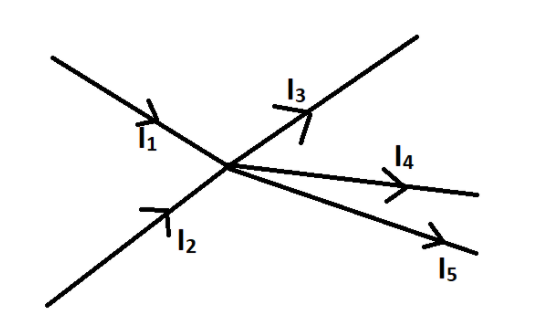
In the above figure, since ${I_1}$, ${I_2}$ are incoming current and ${I_3}$, ${I_4}$, ${I_5}$ are outgoing current, therefore according to Kirchoff's law of junction,
${I_1} + {I_2} = {I_3} + {I_4} + {I_5}$ ---------(1)
Now, we know that, $I = \dfrac{{dq}}{{dt}}$,
So, ${I_1} = \dfrac{{d{q_1}}}{{dt}}$, ${I_2} = \dfrac{{d{q_2}}}{{dt}}$, ${I_3} = \dfrac{{d{q_3}}}{{dt}}$, ${I_4} = \dfrac{{d{q_4}}}{{dt}}$ and ${I_5} = \dfrac{{d{q_5}}}{{dt}}$,
Using above in equation $1$,
$\dfrac{{d{q_1}}}{{dt}} + \dfrac{{d{q_2}}}{{dt}} = \dfrac{{d{q_3}}}{{dt}} + \dfrac{{d{q_4}}}{{dt}} + \dfrac{{d{q_5}}}{{dt}}$
On simplifying we get,
$d{q_1} + d{q_2} = d{q_3} + d{q_4} + d{q_5}$ -------(2)
Now, we know that $\int_0^x {dx} = x$,
So on integrating equation $2$, we get,
$\int_0^{{q_1}} {d{q_1}} + \int_0^{{q_2}} {d{q_2}} = \int_0^{{q_3}} {d{q_3}} + \int_0^{{q_4}} {d{q_4}} + \int_0^{{q_5}} {d{q_5}}$
So, on simplifying we get,
${q_1} + {q_2} = {q_3} + {q_4} + {q_5}$,
This proves that the Kirchoff's law of junction tells about the conservation of charge.

So correct option in Option (B).

Note In equation $2$, we do not have integral constant, because the integration was definite. This law of Kirchoff is very useful in solving circuits as it gives us the equation for finding current. The number of equations by this law will be equal to the number of junctions in the circuit.