Question

Kirchhoff’s rules are very useful for analysis of electrical circuits. State Kirchhoff’s junction rules.

Answer 1

Hint: We know that current and voltages in a simple circuit can be found by using ohm’s law. For a complex electrical circuit, ohm’s law is not applicable to do calculations and find current and voltage equation in a circuit like bridge network, T-network etc. to do these types of calculations we used Kirchhoff’s law. Kirchhoff’s laws, when applied to solve electrical networks, are also known as Kirchhoff’s rule.

Complete step by step answer:
A German physicist, Gustav Kirchhoff developed a pair or set of rules which deal with the conservation of current and energy within the electrical circuits. These two rules are:
1. Kirchhoff’s current or junction law (KCL)
It states that the sum of all the currents entering any point or junction must be equal to the sum of all currents leaving that point junction. It is based on the law of conservation of charges.
i.e. $\sum I$ = $0$

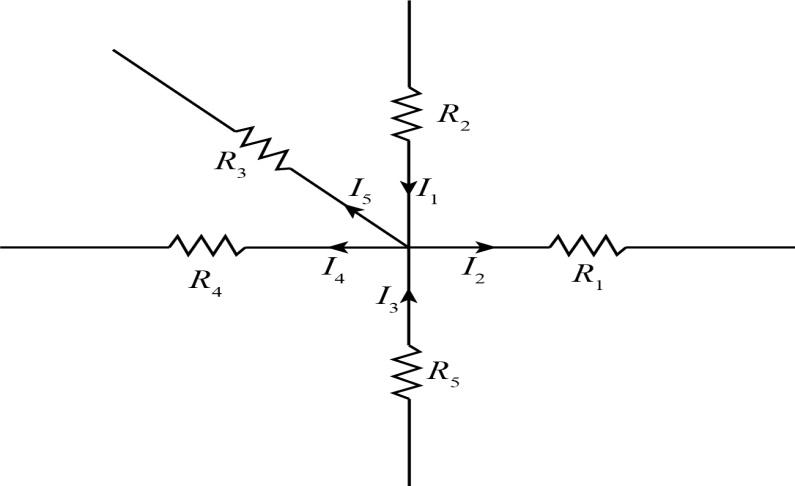
Consider a point O in an electrical circuit. Let $I_1$, $I_3$ be the currents entering the point O and $I_2$, $I_4$, $I_5$ be the currents leaving the point O. Then according to Kirchhoff’s first law,
\eqalign{ & {I_1} + {I_3} = {I_2} + {I_4} + {I_5} \cr & \cr & {I_1} + {I_3} - {I_2} - {I_4} - {I_5} = 0 \cr & \cr & \therefore \sum I = 0 \cr}
Thus current entering the point can be taken as positive while currents were leaving the point taken as negative.
ii) Kirchhoff’s second law (voltage law)(KVL)
It states that the algebraic sum of all voltages, i.e. the potential differences across all elements and e.m.f’s of all sources in any closed electrical circuit is zero. It is based on the law of conservation of energy.
i.e. $\sum E + \sum \Delta V = 0$
When applying Kirchhoff’s second rule, the loop rule, you must identify a closed-loop and decide in which direction to go around it, clockwise or counterclockwise. The loop was traversed in the same direction as the current (clockwise).

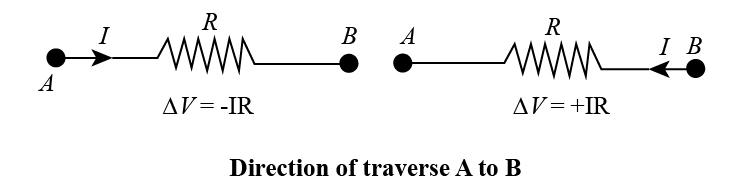
When a resistor is traversed within the equivalent direction to the current, the present change in potential is −IR.
When a resistor is traversed within the direction opposite to the current, the change in potential is +IR.
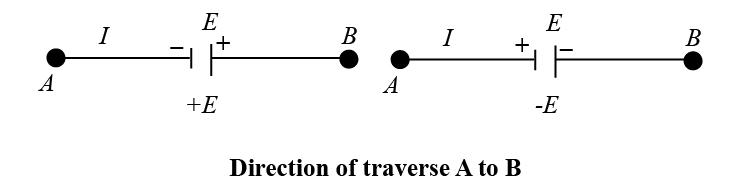
When an e.m.f is traversed from – to + (the same direction it moves positive charge), the change in potential is +e.m.f.
When an emf is traversed from + to – (opposite to the direction it moves positive charge), the change in potential is – e.m.f.

Note: KCL and KVL aren’t good for high-frequency AC circuits. KCL is valid as long as the entire electric charge is constant within the circuit.