Question

Kepler's second law is a consequence of
(A) Conservation of energy
(B) Conservation of linear momentum
(C) Conservation of angular momentum
(D) Conservation of mass

Answer 1

Kepler's second law states that the planet moves in an elliptical orbit such that the line between it and the Sun placed at a focus sweeps out equal areas in equal times. Conservation of angular momentum states that the angular momentum of a body remains constant unless an external torque is applied.
Formula used:
The area of the triangle/wedge is $A=\dfrac{1}{2} \times base \times height$
$r\dfrac{{d\theta }}{{dt}} = v$ (Where $v$ is linear velocity, $d\theta$ is an elemental angle which we have considered, $r$ is the radius of the orbit of which the wedge is a part and$dt$is the elemental time in which our observation is made.)
$L = m(r \times v)$(Where $L$ is angular momentum)

Complete step-by-step answer:

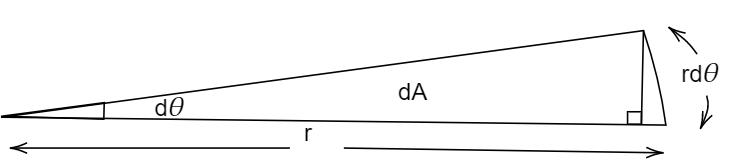
Consider a small wedge of the orbit traced out in time $dt$, $d\theta$ is an elemental angle which we have considered, $r$ is the radius of the orbit of which the wedge is a part
So,
Area of the wedge is, $A=\dfrac{1}{2} \times base \times height$
The base is $r$ and height is $rd\theta$, $dA$ is the area of the wedge,
$\Rightarrow dA = \dfrac{1}{2}r \times rd\theta$
The rate at which area is swept out is,
$\Rightarrow \dfrac{{dA}}{{dt}} = \dfrac{1}{2}r \times r\dfrac{{d\theta }}{{dt}}$
since $r\dfrac{{d\theta }}{{dt}} = v$ , where $v$ is linear velocity, $\theta$ is the angle between $r$ and $v$
$\Rightarrow \dfrac{{dA}}{{dt}} = \dfrac{1}{2}rv\theta$
We know that,
$L$ Is angular momentum and m is the mass of the object
$\Rightarrow L = m(r \times v)$
$\Rightarrow L = mrv \sin \theta$

As $\theta$ is very small, $\sin \theta \simeq \theta$
$\Rightarrow L = mrv\theta$
From the above equation, we can draw that,
$\Rightarrow \dfrac{{dA}}{{dt}} = \dfrac{1}{2}\dfrac{L}{m}$
Hence $\dfrac{{dA}}{{dt}}$ is constant with time as $L$ is constant (from conservation of angular momentum) and mass is also constant. This is what Kepler stated in his second law.

Hence option (C) Conservation of angular momentum is the correct answer.

Note
Kepler gave three such laws on the planetary motion we just saw and proved the second law given by Kepler. The first law explained that the earth moves in an elliptical orbit and the sun is present at one of the foci of that ellipse. The third law gave the relation between the length of the semi-major axis of an ellipse about which earth is moving and the time period of this motion.