Question

Kellogg is a new cereal formed of a mixture of bran and rice that contains at least $88$ grams of protein and at least $36$ milligrams of iron. Knowing that bran contains $80$ grams of proteins and $40$ milligrams of iron per kilogram, and that rice contains $100$ grams of protein and $30$ milligrams of iron per kilogram. Find the minimum cost of producing this new cereal if bran costs ₹ $5$ per kilogram and rice costs ₹ $4$ per kilogram.
A) ₹ $4.8$
B) ₹ $4.6$
C) ₹ $3.2$
D) ₹ $4$

Answer 1

For solving this particular question , we have to form equations from the given information and then try to plot the equation of lines . Find the corner points in the graph then evaluate which corner point gives the minimum cost.

Complete step by step solution:
Let the units of bran be $x$ kg , and the units of rice be $y$ kg. We know that,

| Protein | Iron | Cost
---|---|---|---
Bran | 80| 40| 5
Rice| 100| 30| 4
Availability minimum| 88| 36|

We have to minimize $Z = 5x + 4y$
According to the question we have three constraints ,
$80x + 100y \geqslant 88.......(1) \\\ 40x + 30y \geqslant 36........(2) \\\ x,y \geqslant 0....................(3) \\\$
Now consider $80x + 100y = 88$ ,

x	0	1.1
y	22/25	0

we have , $(0,0.8)$ and $(1,0)$ .
$40x + 30y = 36$

x	0	0.9
y	1.2	0

we have , $(0,1.2)$ and $(0.9,0)$.

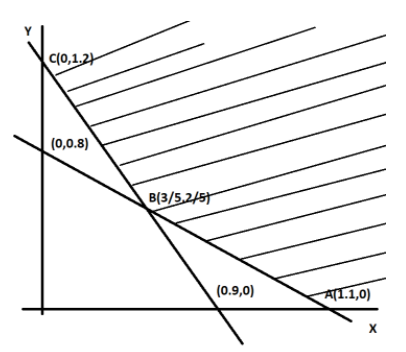
Corner points	Z=5x+4y
A(1.1,0)	Z=5.5
B(3/5,2/5)	Z=23/5=4.6
C(0,1.2)	Z=4.8

From the table it is clear that $Z$ is minimum at $B\left( {\dfrac{3}{5},\dfrac{2}{5}} \right)$
${Z_{\min }} = 4.6$

Therefore, option $B$ is the correct option.

Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. With the help of the graph, we can easily get the corner points , once we get the corner points we can find the point according to the given constraints.