Question

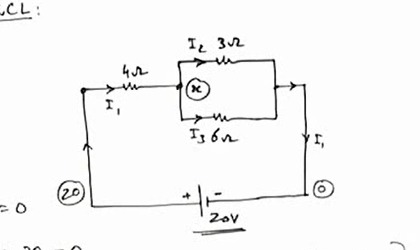
KCL: $I_2$ 3$\Omega$ 4$\Omega$ $I_1$ x $I_3$ 6$\Omega$ $I_1$ 20V 20 0

• A. The value of current $I_1$ is $\frac{10}{3}A$.
• B. The value of current $I_1$ is $5A$.
• C. The value of current $I_1$ is $2A$.
• D. The value of current $I_1$ is $10A$.

Answer 1

Answer: (A)

The value of current $I_1$ is $\frac{10}{3}A$.

Answer 2

The circuit consists of a 20V battery connected to a 4$\Omega$ resistor in series with a parallel combination of a 3$\Omega$ and a 6$\Omega$ resistor.

1. Calculate the equivalent resistance of the parallel resistors: $R_{parallel} = \frac{3\Omega \times 6\Omega}{3\Omega + 6\Omega} = \frac{18}{9}\Omega = 2\Omega$
2. Calculate the total resistance of the circuit: $R_{total} = 4\Omega + R_{parallel} = 4\Omega + 2\Omega = 6\Omega$
3. Calculate the total current $I_1$ flowing from the battery using Ohm's Law: $I_1 = \frac{V}{R_{total}} = \frac{20V}{6\Omega} = \frac{10}{3}A$
4. At node 'x', Kirchhoff's Current Law (KCL) states that the sum of currents entering the node equals the sum of currents leaving the node. Thus, $I_1 = I_2 + I_3$.

Given the ambiguity of the question "KCL:", and assuming a numerical answer is expected in the context of JEE/NEET, the most fundamental current to solve for is $I_1$.