Question

Factorize the expression $k^4 + k^2 + 1$.

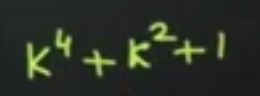
• A. $(k^2 - k + 1)(k^2 + k + 1)$
• B. $(k^2 + 1)^2$
• C. $(k^2 - 1)(k^2 + 1)$
• D. $(k+1)^4$

Answer 1

Answer: (A)

(k^2 - k + 1)(k^2 + k + 1)

Answer 2

To factorize the expression $k^4 + k^2 + 1$, we can use the technique of completing the square.

1. Add and subtract $k^2$ to the expression: $k^4 + k^2 + 1 = k^4 + 2k^2 + 1 - k^2$
2. Group the first three terms, which form a perfect square trinomial: $(k^4 + 2k^2 + 1) - k^2$
3. Recognize the perfect square $(k^2 + 1)^2$: $(k^2 + 1)^2 - k^2$
4. Apply the difference of squares formula, $A^2 - B^2 = (A - B)(A + B)$, where $A = k^2 + 1$ and $B = k$: $((k^2 + 1) - k)((k^2 + 1) + k)$
5. Rearrange the terms within each parenthesis to get the standard form: $(k^2 - k + 1)(k^2 + k + 1)$ The factors $k^2 - k + 1$ and $k^2 + k + 1$ are irreducible over real numbers as their discriminants are negative.