Question
Question: Jump of discontinuity of f(x) = $\frac{(e^{tan x} - 1)}{(e^{tan x} + 1)}$ at x = $\frac{\pi}{2}$ is...
Jump of discontinuity of f(x) = (etanx+1)(etanx−1) at x = 2π is
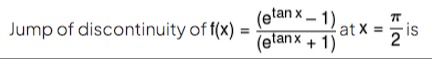
2
Solution
Let the given function be f(x)=(etanx+1)(etanx−1). We need to find the jump of discontinuity at x=2π.
The jump of discontinuity at a point x=a is defined as the absolute difference between the right-hand limit and the left-hand limit at that point, i.e., ∣limx→a+f(x)−limx→a−f(x)∣.
First, we calculate the left-hand limit at x=2π: LHL=limx→(π/2)−f(x)=limx→(π/2)−etanx+1etanx−1
As x→(2π)−, tanx→+∞.
Let y=tanx. As x→(2π)−, y→+∞.
LHL=limy→+∞ey+1ey−1
To evaluate this limit, divide the numerator and the denominator by ey: LHL=limy→+∞1+e−y1−e−y
As y→+∞, e−y→0.
LHL=1+01−0=1.
Next, we calculate the right-hand limit at x=2π: RHL=limx→(π/2)+f(x)=limx→(π/2)+etanx+1etanx−1
As x→(2π)+, tanx→−∞.
Let y=tanx. As x→(2π)+, y→−∞.
RHL=limy→−∞ey+1ey−1
As y→−∞, ey→0.
RHL=0+10−1=−1.
Since the left-hand limit (1) and the right-hand limit (−1) exist but are not equal, the function has a jump discontinuity at x=2π.
The jump of discontinuity is the absolute difference between the right-hand limit and the left-hand limit: Jump =∣RHL−LHL∣=∣−1−1∣=∣−2∣=2.
