Question
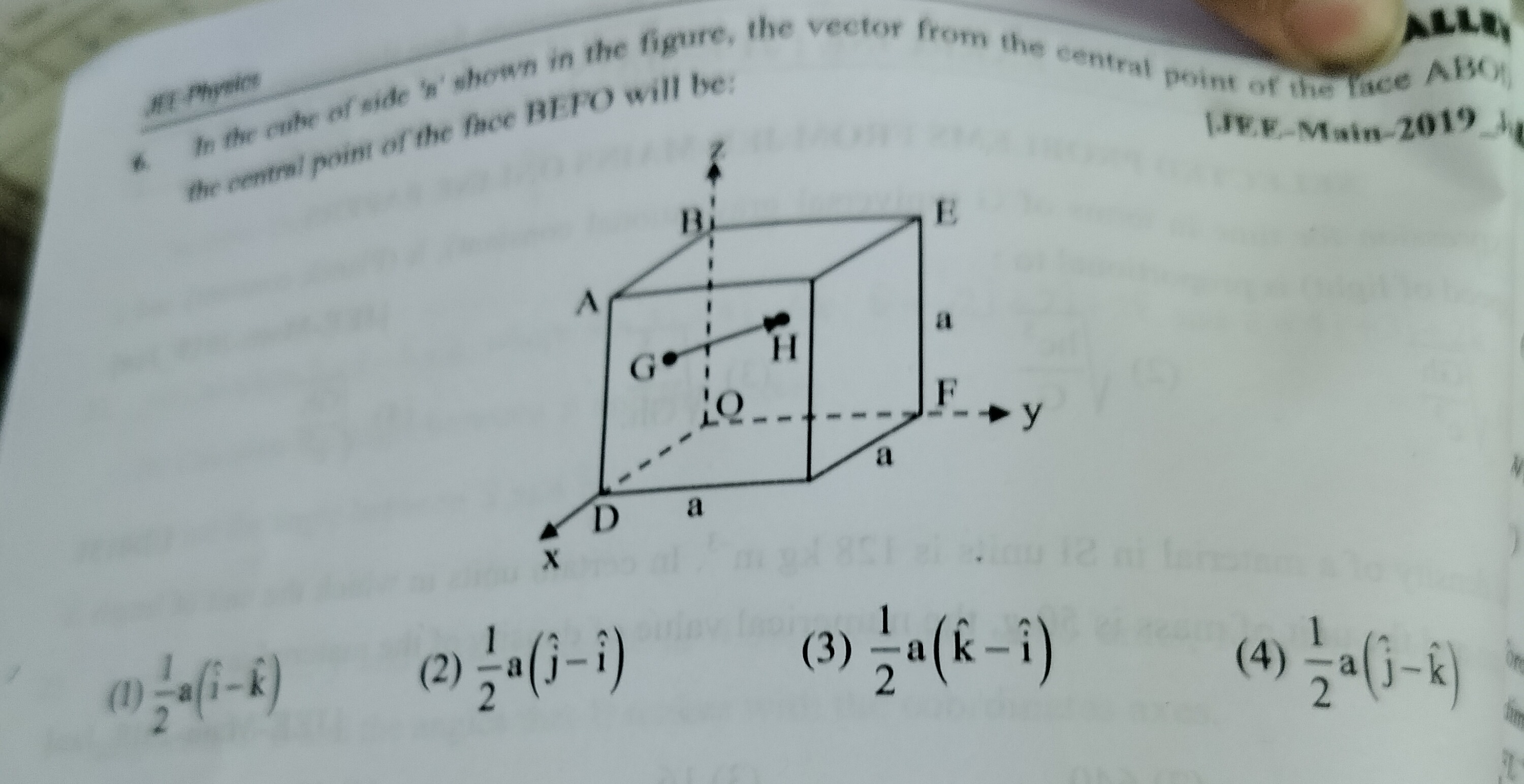
Question: In the cube of side 'a' shown in the figure, the vector from the central point of the face ABO the c...
In the cube of side 'a' shown in the figure, the vector from the central point of the face ABO the central point of the face BEFO will be: [JEE-Main-2019]
21a(i^−k^)
21a(j^−i^)
21a(k^−i^)
21a(j^−k^)
21a(j^−i^)
Solution
The cube has side length 'a'. We set up a coordinate system with the origin O at (0,0,0). Let the x-axis be along OD, the y-axis along OF, and the z-axis along OB.
The coordinates of the vertices are: O = (0, 0, 0) D = (a, 0, 0) F = (0, a, 0) B = (0, 0, a) A = (a, 0, a) (vertex above D) E = (0, a, a) (vertex above F) H = (a, a, a) (vertex above C, where C=(a,a,0))
The first face mentioned is ABO. Based on the figure and the context of a cube, this is likely a typo and refers to the face ODBA, which is in the xz-plane (y=0). The vertices are O(0,0,0), D(a,0,0), B(0,0,a), A(a,0,a). The central point of this face, let's call it C1, is the average of the coordinates of its vertices: C1=4(0,0,0)+(a,0,0)+(0,0,a)+(a,0,a)=4(2a,0,2a)=(2a,0,2a). The position vector of C1 is r1=2ai^+2ak^.
The second face mentioned is BEFO. This is the face in the yz-plane (x=0). The vertices are B(0,0,a), E(0,a,a), F(0,a,0), O(0,0,0). The central point of this face, let's call it C2, is the average of the coordinates of its vertices: C2=4(0,0,a)+(0,a,a)+(0,a,0)+(0,0,0)=4(0,2a,2a)=(0,2a,2a). The position vector of C2 is r2=2aj^+2ak^.
The vector from the central point of face ABO (interpreted as ODBA) to the central point of face BEFO is C1C2=r2−r1. r2−r1=(0i^+2aj^+2ak^)−(2ai^+0j^+2ak^) =(0−2a)i^+(2a−0)j^+(2a−2a)k^ =−2ai^+2aj^+0k^ =2a(j^−i^).
Comparing this with the given options: (1) 21a(i^−k^) (2) 21a(j^−i^) (3) 21a(k^−i^) (4) 21a(j^−k^)
Our result matches option (2).
The final answer is 21a(j^−i^).
Explanation of the solution:
- Set up a coordinate system with the origin at one vertex of the cube and the axes along the edges.
- Determine the coordinates of the vertices of the two faces mentioned in the question. Assume face ABO is a typo for face ODBA (in the xz-plane) based on the figure and similar questions.
- Calculate the coordinates of the central point of each face by finding the average of the coordinates of its vertices.
- Determine the position vectors of the central points.
- Calculate the vector from the first central point to the second central point by subtracting the position vectors.
The final answer is 21a(j^−i^).
