Question
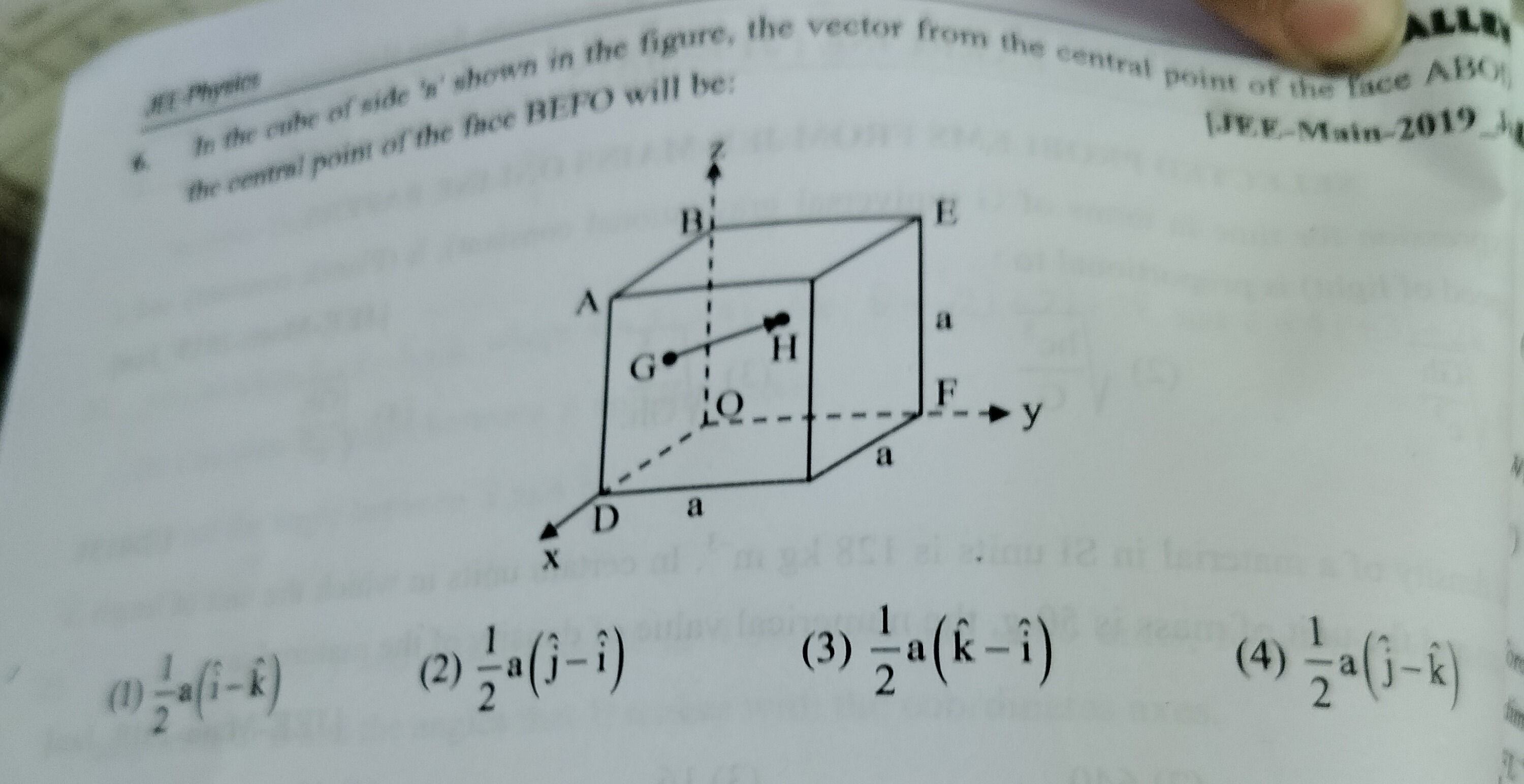
Question: In the cube of side 'a' shown in the figure, the vector from the central point of the face ABO the c...
In the cube of side 'a' shown in the figure, the vector from the central point of the face ABO the central point of the face BEFO will be:
21a(i^−k^)
21a(j^−i^)
21a(k^−i^)
21a(j^−k^)
21a(j^−i^)
Solution
The vertices of the cube are labeled in the figure. We assume the origin O is at (0,0,0). The side length of the cube is 'a'. From the figure, OD is along the x-axis, OF is along the y-axis, and OB is along the z-axis.
So, the coordinates of the vertices are: O = (0,0,0) D = (a,0,0) F = (0,a,0) B = (0,0,a)
Based on the standard labeling of a cube relative to the axes, and the connections shown in the figure: A is connected to O, D, B. From the figure, A appears to be the vertex (a,0,a). G is connected to D, F, H. From the figure, G appears to be the vertex (a,a,0). E is connected to F, B, H. From the figure, E appears to be the vertex (0,a,a). H is connected to A, G, E, B, D, F. H is the vertex opposite to O, so H = (a,a,a).
Let's verify the face names given in the similar question, which seems to correct the likely typo in the original question. The similar question refers to face ABOD and face BEFO. Let's assume the first face is ABOD. Vertices are A=(a,0,a), B=(0,0,a), O=(0,0,0), D=(a,0,0). This is the face OADB, which is in the xz plane (y=0). The central point of face OADB is the average of the coordinates of its vertices: C1=4(0,0,0)+(a,0,a)+(a,0,0)+(0,0,a)=4(0+a+a+0,0+0+0+0,0+a+0+a)=(42a,40,42a)=(2a,0,2a). In vector form, r1=2ai^+0j^+2ak^=2a(i^+k^).
Let's assume the second face is BEFO. Vertices are B=(0,0,a), E=(0,a,a), F=(0,a,0), O=(0,0,0). This is the face OFEB, which is in the yz plane (x=0). The central point of face OFEB is the average of the coordinates of its vertices: C2=4(0,0,0)+(0,0,a)+(0,a,a)+(0,a,0)=4(0+0+0+0,0+0+a+a,0+a+a+0)=(40,42a,42a)=(0,2a,2a). In vector form, r2=0i^+2aj^+2ak^=2a(j^+k^).
The question asks for the vector from the central point of the first face to the central point of the second face. Vector = r2−r1=2a(j^+k^)−2a(i^+k^)=2a(j^+k^−i^−k^)=2a(j^−i^).
