Solveeit Logo
Login

Question

Question: Prove the identity; $\log_a N. \log_b N + \log_b N. \log_c N + \log_c N. \log_a N = \frac{\log_a N. ...

Prove the identity; log⁡aN.log⁡bN+log⁡bN.log⁡cN+log⁡cN.log⁡aN=log⁡aN.log⁡bN.log⁡cNlog⁡abcN\log_a N. \log_b N + \log_b N. \log_c N + \log_c N. \log_a N = \frac{\log_a N. \log_b N. \log_c N}{\log_{abc} N}

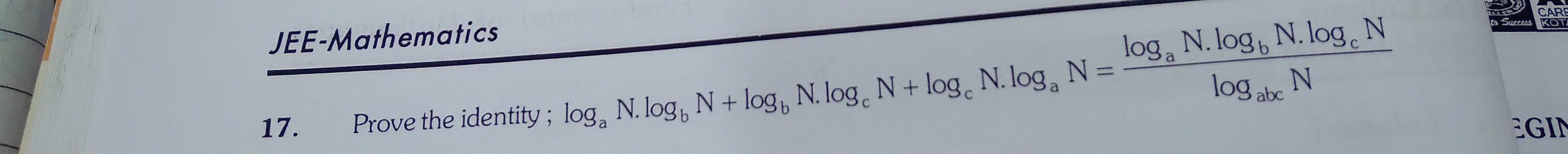
Answer

The identity is proved by using the change of base formula for logarithms and algebraic manipulation of the terms.

Explanation

Solution

Let X=log⁡NaX = \log_N a, Y=log⁡NbY = \log_N b, Z=log⁡NcZ = \log_N c. Then log⁡aN=1/X\log_a N = 1/X, log⁡bN=1/Y\log_b N = 1/Y, log⁡cN=1/Z\log_c N = 1/Z. LHS = 1XY+1YZ+1ZX=X+Y+ZXYZ\frac{1}{XY} + \frac{1}{YZ} + \frac{1}{ZX} = \frac{X+Y+Z}{XYZ}. RHS = (1/X)(1/Y)(1/Z)log⁡abcN=1/(XYZ)1/(log⁡Na+log⁡Nb+log⁡Nc)=1/(XYZ)1/(X+Y+Z)=X+Y+ZXYZ\frac{(1/X)(1/Y)(1/Z)}{\log_{abc} N} = \frac{1/(XYZ)}{1/(\log_N a + \log_N b + \log_N c)} = \frac{1/(XYZ)}{1/(X+Y+Z)} = \frac{X+Y+Z}{XYZ}. Thus, LHS = RHS.