Question

2 NOBr (g) $\rightleftharpoons$ 2 NO (g) + Br₂(g). If nitrosyl bromide (NOBr) is (100/3)% dissociated at 25° C and a total pressure of 0.28 atm. Calculate Kₚ for the dissociation at this temperature.

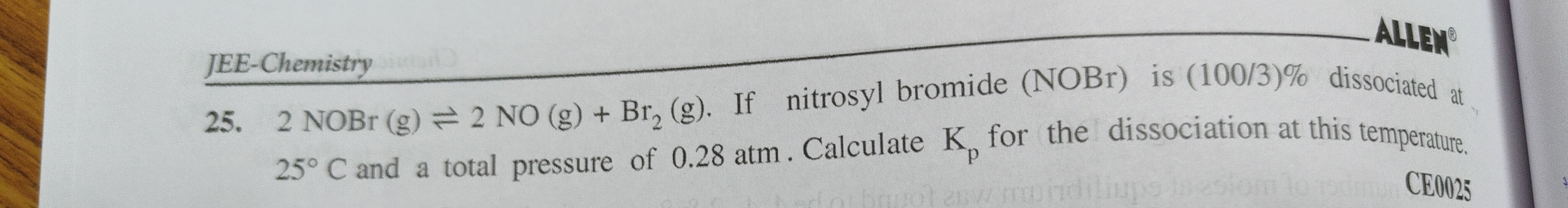
• A. (100/3)% dissociated means $\alpha = 1/3$. Initial pressure: $P_{NOBr} = P_0$ Equilibrium pressures: $P_{NOBr} = P_0(1 - \alpha)$ $P_{NO} = P_0\alpha$ $P_{Br_2} = P_0\alpha/2$ Total pressure $P_{total} = P_{NOBr} + P_{NO} + P_{Br_2} = P_0(1 - \alpha + \alpha + \alpha/2) = P_0(1 + \alpha/2)$ Given $P_{total} = 0.28$ atm and $\alpha = 1/3$. $0.28 = P_0(1 + (1/3)/2) = P_0(1 + 1/6) = P_0(7/6)$ $P_0 = 0.28 \times (6/7) = 0.04 \times 6 = 0.24$ atm. Equilibrium partial pressures: $P_{NOBr} = 0.24(1 - 1/3) = 0.24(2/3) = 0.16$ atm $P_{NO} = 0.24(1/3) = 0.08$ atm $P_{Br_2} = 0.24(1/3)/2 = 0.24(1/6) = 0.04$ atm $K_p = \frac{(P_{NO})^2 \times P_{Br_2}}{(P_{NOBr})^2} = \frac{(0.08)^2 \times 0.04}{(0.16)^2} = \frac{0.0064 \times 0.04}{0.0256} = \frac{0.000256}{0.0256} = 0.01$ atm
• B. 0.02 atm
• C. 0.005 atm
• D. 0.015 atm

Answer 1

Answer: (A)

0.01 atm

Answer 2

The reaction is $2 NOBr (g) \rightleftharpoons 2 NO (g) + Br_2(g)$. Let the initial pressure of NOBr be $P_0$. Given the degree of dissociation $\alpha = (100/3)\% = 1/3$.

At equilibrium, the partial pressures are: $P_{NOBr} = P_0(1-\alpha)$ $P_{NO} = P_0\alpha$ $P_{Br_2} = P_0\alpha/2$

The total pressure is $P_{total} = P_{NOBr} + P_{NO} + P_{Br_2} = P_0(1-\alpha) + P_0\alpha + P_0\alpha/2 = P_0(1 + \alpha/2)$.

Given $P_{total} = 0.28$ atm and $\alpha = 1/3$: $0.28 = P_0(1 + (1/3)/2)$ $0.28 = P_0(1 + 1/6)$ $0.28 = P_0(7/6)$ $P_0 = 0.28 \times (6/7) = 0.04 \times 6 = 0.24$ atm.

Now, calculate the equilibrium partial pressures: $P_{NOBr} = 0.24(1 - 1/3) = 0.24(2/3) = 0.16$ atm $P_{NO} = 0.24(1/3) = 0.08$ atm $P_{Br_2} = 0.24(1/3)/2 = 0.24(1/6) = 0.04$ atm

The equilibrium constant $K_p$ is calculated as: $K_p = \frac{(P_{NO})^2 \times P_{Br_2}}{(P_{NOBr})^2}$ $K_p = \frac{(0.08)^2 \times 0.04}{(0.16)^2}$ $K_p = \frac{0.0064 \times 0.04}{0.0256}$ $K_p = \frac{0.000256}{0.0256} = 0.01$ atm