Question

$\int cos(ln x)dx$

Answer 1

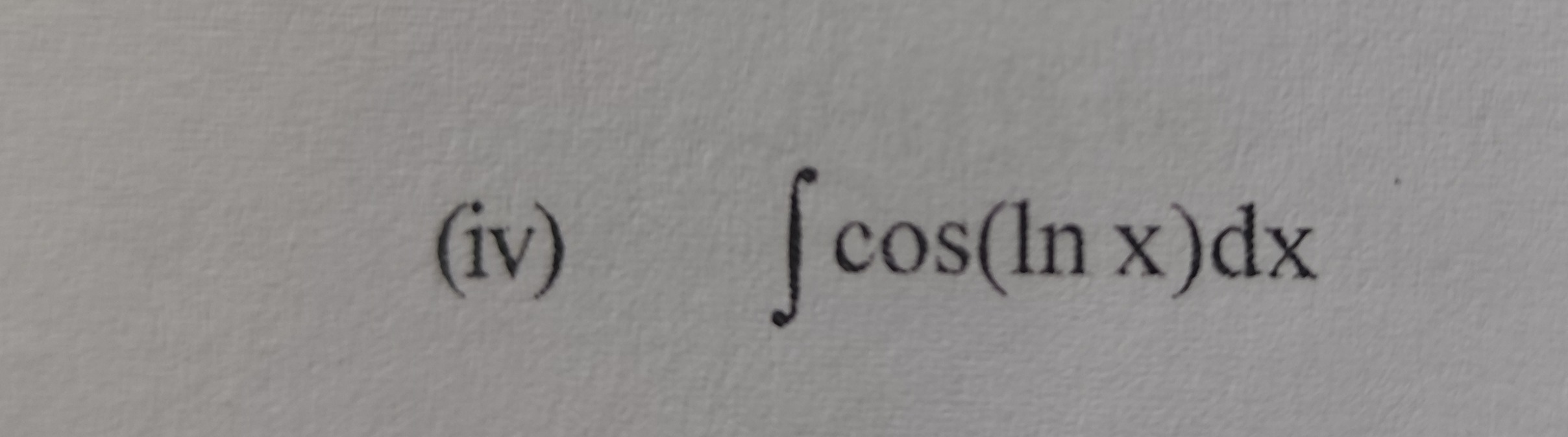
$\frac{x}{2}(\cos(\ln x) + \sin(\ln x)) + C$

Answer 2

To evaluate the integral $\int \cos(\ln x) dx$, we can use the method of integration by parts.

Let $I = \int \cos(\ln x) dx$.

We can write the integral as $\int 1 \cdot \cos(\ln x) dx$. Using integration by parts formula $\int u \, dv = uv - \int v \, du$: Let $u = \cos(\ln x)$ and $dv = 1 \, dx$. Then, we find $du$ and $v$: $du = \frac{d}{dx}(\cos(\ln x)) \, dx = -\sin(\ln x) \cdot \frac{1}{x} \, dx$ $v = \int 1 \, dx = x$

Substitute these into the integration by parts formula: $I = x \cos(\ln x) - \int x \left( -\sin(\ln x) \cdot \frac{1}{x} \right) dx$ $I = x \cos(\ln x) - \int (-\sin(\ln x)) dx$ $I = x \cos(\ln x) + \int \sin(\ln x) dx$ (Equation 1)

Now, we need to evaluate the integral $\int \sin(\ln x) dx$. Let's call this $J$. Again, use integration by parts for $J = \int 1 \cdot \sin(\ln x) dx$: Let $u' = \sin(\ln x)$ and $dv' = 1 \, dx$. Then, we find $du'$ and $v'$: $du' = \frac{d}{dx}(\sin(\ln x)) \, dx = \cos(\ln x) \cdot \frac{1}{x} \, dx$ $v' = \int 1 \, dx = x$

Substitute these into the integration by parts formula for $J$: $J = x \sin(\ln x) - \int x \left( \cos(\ln x) \cdot \frac{1}{x} \right) dx$ $J = x \sin(\ln x) - \int \cos(\ln x) dx$

Notice that $\int \cos(\ln x) dx$ is our original integral $I$. So, $J = x \sin(\ln x) - I$. (Equation 2)

Now, substitute Equation 2 back into Equation 1: $I = x \cos(\ln x) + (x \sin(\ln x) - I)$ $I = x \cos(\ln x) + x \sin(\ln x) - I$

Add $I$ to both sides of the equation: $2I = x \cos(\ln x) + x \sin(\ln x)$ $2I = x (\cos(\ln x) + \sin(\ln x))$

Finally, solve for $I$: $I = \frac{x}{2} (\cos(\ln x) + \sin(\ln x)) + C$ where $C$ is the constant of integration.

The integral $\int \cos(\ln x) dx$ is solved using integration by parts twice.

1. First, apply integration by parts to $I = \int 1 \cdot \cos(\ln x) dx$, which leads to $I = x \cos(\ln x) + \int \sin(\ln x) dx$.

2. Then, apply integration by parts again to the new integral $J = \int 1 \cdot \sin(\ln x) dx$, which results in $J = x \sin(\ln x) - \int \cos(\ln x) dx$.

3. Substitute $J$ back into the expression for $I$. This creates an equation where $I$ appears on both sides.

4. Solve the resulting algebraic equation for $I$ to get the final solution.