Question

It is given that $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ are the position vectors of vertices A, B and C respectively of a parallelogram ABCD, find the position vector of D.

Answer 1

Hint: It is given that the three vertices of the parallelogram A, B and C are represented by the vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ respectively. Let us assume that the vertex D is represented by the vector $\overrightarrow{d}$. We know that the diagonals of the parallelogram bisect each other so find the midpoint of the diagonal AC and BD and then equate the midpoint of the diagonal AC with the midpoint of the diagonal BD. By solving this equation we will get the vector $\overrightarrow{d}$.

Complete step by step solution:
In the below diagram we have shown a parallelogram ABCD with vertices A, B, C and D and the diagonals of the parallelogram AC and BD intersect at point E.

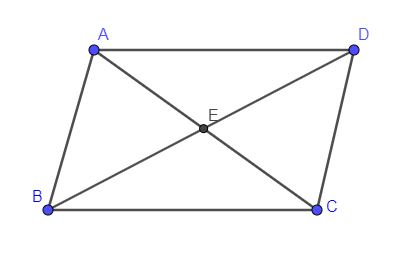
Let us assume that the position vector of vertex D is $\overrightarrow{d}$.
Now, we know that diagonals of a parallelogram bisect each other. It means E is the midpoint of AC and BD. We are going to write the midpoint of AC in terms of $\overrightarrow{a}\And \overrightarrow{c}$ by adding the vectors $\overrightarrow{a}\And \overrightarrow{c}$ and then divide the result of addition of the two vectors by 2.
$E=\dfrac{\overrightarrow{a}+\overrightarrow{c}}{2}$……….. Eq. (1)
Similarly, the midpoint of diagonal BD in terms of position vectors $\overrightarrow{b}\And \overrightarrow{d}$ by adding the vectors $\overrightarrow{b}\And \overrightarrow{d}$ followed by division of the result of addition by 2.
$E=\dfrac{\overrightarrow{b}+\overrightarrow{d}}{2}$………….. Eq. (2)
Equating eq. (1) and eq. (2) we get,
$\dfrac{\overrightarrow{a}+\overrightarrow{c}}{2}=\dfrac{\overrightarrow{b}+\overrightarrow{d}}{2}$
In the above equation, one half will be cancelled on both the sides of the equation.
$\begin{aligned} & \overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d} \\\ & \Rightarrow \overrightarrow{a}+\overrightarrow{c}-\overrightarrow{b}=\overrightarrow{d} \\\ \end{aligned}$
From the above solution, we have got the position vector corresponding to vertex D is:
$\overrightarrow{a}+\overrightarrow{c}-\overrightarrow{b}=\overrightarrow{d}$

Note: This question demands the knowledge of vector addition and the properties of parallelogram like if you don’t know the property of the parallelogram that the diagonals bisect each other then you will be lost in the problem. This is the main requirement to solve the problem. Another point to be noted is that if you don’t know how to add the two vectors then also you get stuck so make sure you will properly learn these two concepts.