Question

It is given that ABC is a right triangle which is right angled at B such that $\angle BCA=2\angle BAC$. Show that hypotenuse of this triangle AC = 2 BC.

Answer 1

Hint: In triangles, we have a property which is called an angle sum property which states that the sum of all the angles of a triangle is equal to 180. Assume a variable x which will represent the measure of $\angle BAC$. So, $\angle BCA$ will be equal to 2x. Use angle sum property to find the value of x. Then using the concepts of trigonometry, we can solve this question.

Complete step-by-step answer:
Before proceeding with the question, we must know all the concepts and formulas that will be required to solve this question.
In triangles, we have an angle sum property which states that the sum of all the angles of any triangle is equal to 180 degree . . . . . . . . . . . . . . (1)
In trigonometry, the cosine for an angle in a right triangle is given by the ratio of the base and the hypotenuse . . . . . . . . . . . . . (2)
In this question, we are given that ABC is a right triangle which is right angled at B such that $\angle BCA=2\angle BAC$. We are required to show that AC = 2 BC.

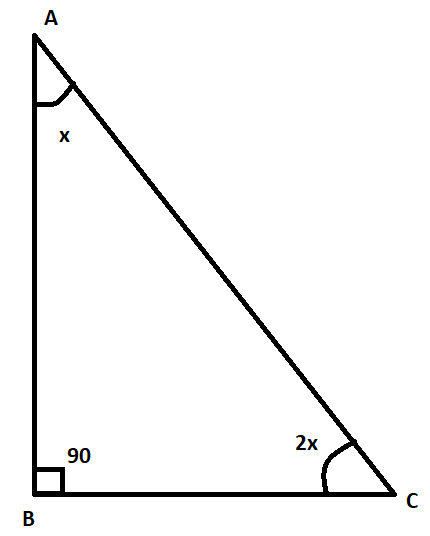
Let us assume that $\angle BAC$ = x. Since $\angle BCA=2\angle BAC$, we can say that $\angle BCA$. Also, it is given that $\angle B=90$. From (1), using angle sum property in this triangle, we get,
x + 2x + 90 = 180
$\Rightarrow$ 3x = 90
$\Rightarrow$ x = 30
$\Rightarrow \angle BAC=30,\angle BCA=60$
From formula (2), applying cos function on angle BCA, we get,
$\cos {{60}^{\circ }}=\dfrac{BC}{AC}$

From trigonometry, we have $\cos {{60}^{\circ }}=\dfrac{1}{2}$.
$\begin{aligned} & \Rightarrow \dfrac{1}{2}=\dfrac{BC}{AC} \\\ & \Rightarrow AC=2BC \\\ \end{aligned}$
Hence, proved.

Note: There is a possibility that one may proceed with this question by using Pythagoras theorem since it is a right triangle. But since there is no relation given between the sides AB and BC, we cannot find the answer to this question by using Pythagoras theorem.