Question
Question: It has been mentioned in the question that the angle between two mirrors placed together will be \(\...
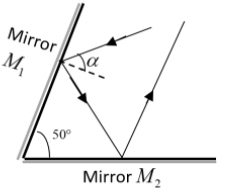
It has been mentioned in the question that the angle between two mirrors placed together will be θ=50∘. Then find the angle α so that the reflected ray is parallel to M1.
Solution
Draw a diagram showing the value of angles given. As we all know that the angle of incidence will be equivalent to the angle of reflection. Therefore the angle between the reflected ray and the mirror M2 will be the same as the angle between the mirrors. The sum of the angle of a triangle will be equivalent to 180∘. This will help you in answering this question.
Complete answer:
First of all, draw a diagram showing the value of angles that we know already as per the question.
The angle between the two mirrors are mentioned as,
θ=50∘
The angle of incidence of the first ray coming has been given as α.
As we all know that the angle of incidence will be equivalent to the angle of reflection in general. Therefore the angle of reflection of that ray from the mirror M1will also be α.
As this angle is α, the angle ABC will be the difference of the 90∘ and α. That is 90−α.
As it is already mentioned in the question that the final reflected ray is parallel to the mirror M1. Therefore the angle between the reflected ray and the mirror will be the same as the angle between the mirrors. That is 50∘.
Therefore the angle of reflection of this ray will be equivalent to the difference between 90∘ and 50∘. That is 40∘.
Thus angle of incidence will also be 40∘. And hence the balance angle will also be 50∘.
As we all know, the sum of the angle of a triangle will be equivalent to 180∘. Therefore we can write that,
