Question
Question: It has been given that two thin convex lenses having focal length \({{f}_{1}}\) and \({{f}_{2}}\). T...
It has been given that two thin convex lenses having focal length f1 and f2. They are separated by a horizontal distance d (where d<f1,d<f2) and their centres are moved by a vertical separation Δ as depicted in the figure. Let us assume the origin of coordinates O at the centre of the first lens. Then for a parallel beam of rays coming from the left, what will be the x and y coordinates of the focal point of this lens system?
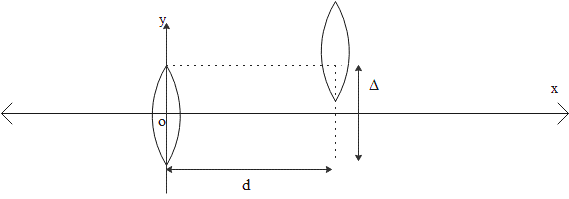
A.x=f1+f2f1f2,y=ΔB.x=f1+f2−df1(f2+d),y=f1+f2ΔC.x=f1+f2−df1f2+d(f1−d),y=f1+f2−dΔ(f1−d)D.x=Δ,y=f1+f2−dΔ(f1−d)
Solution
Using lens equation, first of all find the image distance of the first lens. This image of the first lens can be the object for the second lens. Then apply the lens equation for finding the image distance of the second lens. Then find the coordinates of x and y of the combined mass system.
Complete answer:
let the focal length of the first lens be f1 and that of the second lens be f2.
Using the lens formula for the first lens,
v11−∞1=f11⇒v1=f1
For the second case, we can write that,
The object for the second lens can be the image of the first lens. That is,
u=v1=f1−d
Therefore, we can write that,
v21−f1−d1=f21
That is,
v2=f1+f2−df2(f1−d)
Now let us consider the combined mass system. The x coordinate of this can be written as,
x=v2+d=f1+f2−df1f2+d(f1−d)
Then the y-coordinate can be found from the equation,
Δy1=f1−dv2⇒y1=f1+f2−df2Δ
Therefore the y-coordinate will be given as,
y=Δ−y1⇒y=f1+f2−dΔ(f1−d)
So, the correct answer is “Option C”.
Note:
The lens formula is the basic thing we use in order to solve this question. The reciprocal of the focal length of the lens will be equivalent to the difference between the reciprocal of the image distance and the reciprocal of the object distance. Focal length is the distance from the lens where the clear and perfect image is being formed by the rays from infinity.
