Question

It has been given that two similar cars A and B are moving at $36kmph$. A is climbing on a bridge, convex upward and B on concave upward. Let us assume that if the radius of curvature of bridge be $20m$, the ratio of normal forces exerted on the cars if they are at the middle of bridges $\left( g=10m{{s}^{-2}} \right)$.
$\begin{aligned} & A.1:3 \\\ & B.1:2 \\\ & C.2:3 \\\ & D.1:5 \\\ \end{aligned}$

Answer 1

First of all we have to convert the unit of velocity from kilometre per hour to metre per second. The centripetal force can be found by taking the ratio of the product of the mass and the velocity to the radius of the bridge. Find the normal reaction in each case and take the ratio of them. This will help you in answering this question.

Complete step by step solution:
First of all we have to convert the unit of velocity from kilometre per hour to metre per second. That is we can write that,
$v=36\times \dfrac{5}{18}=10m{{s}^{-1}}$
Then the centripetal force can be found by the equation,
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$
Where $m$ be the mass of the body, $r$ be the radius of the body and $v$ be the velocity.
The radius of curvature of the bridge has been given as,
$r=20m$
Substituting the values in it,
${{F}_{C}}=\dfrac{m\times {{10}^{2}}}{20}=5m$
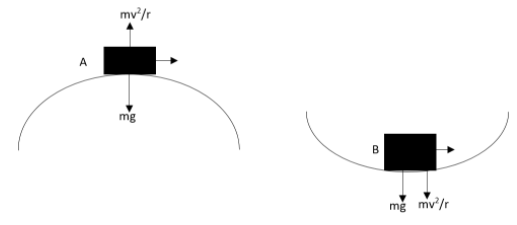
In the case of A, bridge is convex upward, then the normal reaction there will be given as,
${{N}_{A}}=mg-{{F}_{C}}$
Substituting the values in it will give,
${{N}_{A}}=10m-5m=5m$
In the case of B, bridge is concave upward, then the normal reaction there will be found to be as,
${{N}_{B}}=mg+{{F}_{C}}$
Substituting the values in it will give,
${{N}_{B}}=10m+5m=15m$
Taking the ratio of both these normal forces will give us the answer. That is,
${{N}_{A}}:{{N}_{B}}=5:15=1:3$
The answer for the question has been calculated.

The answer has been mentioned as option A.

Note:
Centripetal force is the force formed when a body is moving in a circular path. The direction of motion of this body will always be perpendicular to the motion of the body and this will be towards the centre position also. The unit of centripetal force is the same as that of normal force.