Question

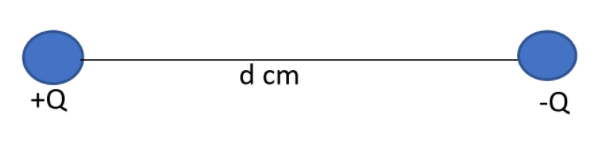
It has been given that two identical spheres, one positively charged and the other negatively charged are kept$dcm$ apart. When the magnitude of the charges on the two spheres will be equivalent, calculate the electric potential at a point midway on the line joining the centres of the two spheres.
$\begin{aligned} & A.0 \\\ & B.10V \\\ & C.5V \\\ & D.1.6\times {{10}^{-19}}V \\\ \end{aligned}$

Answer 1

The potential at this point can be found by taking the ratio of the charge located at this point to the product of the constant $4\pi {{\varepsilon }_{0}}$ and the distance to this point. Now, at the point midway between the spheres, the distance from the centre of both the spheres will be equivalent. That is we can say that $r$. Using this, find the potential at the midway. This will help you in answering this question.

Complete step by step answer:
Let us assume that the charge on the first sphere be $Q$ and on the second sphere be given as $-Q$.
The potential at this point can be found by taking the ratio of the charge located at this point to the product of the constant $4\pi {{\varepsilon }_{0}}$ and the distance to this point. This can be shown as an equation given as,
$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{r}$
Now, at the point midway between the spheres, the distance from the centre of both the spheres will be equivalent. That is we can say that $r$. Therefore the resultant field at the midpoint can be written as,
$\begin{aligned} & V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{r}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{-Q}{r} \\\ & \therefore V=0 \\\ \end{aligned}$
Therefore the potential at this point has been found to be zero.

So, the correct answer is “Option A”.

Note: An electric potential can be otherwise known as the electric field potential or the electrostatic potential. This can be defined as the amount of work required in order to move a unit of electric charge from a reference location to a particular position in an electric field without developing an acceleration. In general this reference point has been taken as the earth or at infinity.