Question

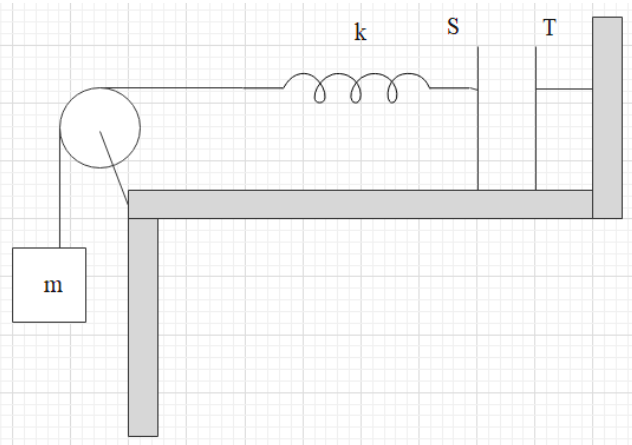
It has been given that the plates S and T of an uncharged parallel plate capacitor have been connected across a battery. The battery is made disconnected then and the charged plates get connected in a system as represented in the diagram. The system given is in equilibrium. All the strings are insulating and massless. What will be the magnitude of the charge on one of the capacitor plates?
Note that the area of plates $=A$

$\begin{aligned} & A.\sqrt{2mgA{{\varepsilon }_{0}}} \\\ & B.\sqrt{\dfrac{4mgA{{\varepsilon }_{0}}}{k}} \\\ & C.\sqrt{mgA{{\varepsilon }_{0}}} \\\ & D.\sqrt{\dfrac{2mgA{{\varepsilon }_{0}}}{k}} \\\ \end{aligned}$

Answer 1

Here in this question the whole system is in equilibrium so the tension will be equal to the weight of the block and the electrostatic force of the parallel plate capacitor. The weight of the block should be equal to the force of spring and the system should be considered in equilibrium. The electrostatic force of the parallel plate capacitor should be calculated in order to find the magnitude of the charge on the capacitor plates.

Complete step-by-step solution
Here it is given that this is a parallel plate capacitor with plates S and T connected across a battery. After charging the battery is disconnected and now the charged plates are now connected as shown in the system. Here the plate S of the capacitor is connected with a spring of spring constant $k$ further, the spring is connected to a block of mass $m$. The area of plates has been given as $A$.
In the system after some time, this will be in equilibrium and the plates will be steady. Therefore now the free body diagram of the block will be,

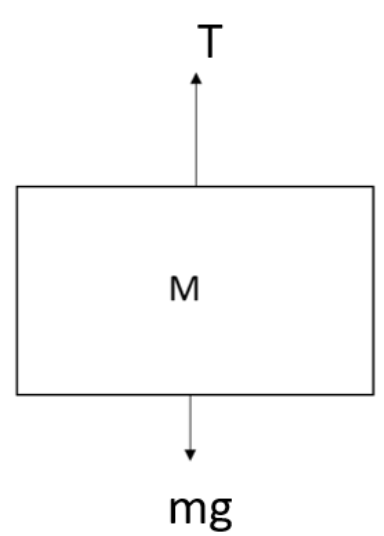
Here we can write that,
$T=mg.........\left( 1 \right)$
Where $T$ be the tension and $mg$ be the weight of the block.
Now as the block is connected to the plates through a spring, tension is equal to the force exerted by the spring. That is,
$\therefore T=kx.........\left( 2 \right)$
Where $x$ represents the elongation of the spring.
Now from equation 1 and 2 we can write that,
$mg=kx.........\left( 3 \right)$
Now as we know electrostatic charge density will be applied between the plates of capacitor can be shown as,
$E=\dfrac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}..........\left( 4 \right)$
Where $\sigma$ be the charge density per unit area, ${{\varepsilon }_{0}}$ be permeability.
And also we know that,
$\sigma =\dfrac{Q}{A}$
From the equation 4 we can write that,
$E=\dfrac{{{Q}^{2}}}{2{{\varepsilon }_{0}}{{A}^{2}}}.......(5)$
The electrostatic force will be the product of the energy density and the area. That is we can write that,
$F=E\times A=\dfrac{{{Q}^{2}}}{2{{\varepsilon }_{0}}{{A}^{2}}}\times A=\dfrac{{{Q}^{2}}}{2{{\varepsilon }_{0}}A}$
In equilibrium,
$\dfrac{{{Q}^{2}}}{2{{\varepsilon }_{0}}A}=mg$
Rearranging the equation,
$Q=\sqrt{2mgA{{\varepsilon }_{0}}}$
Therefore the correct answer has been obtained as option A.

Note: A capacitor is an electrical device which collects electrical energy in an electrical field. It is a passive electronic component with two end terminals. There are usually parallel plates, spherical and cylindrical types of capacitors.