Question

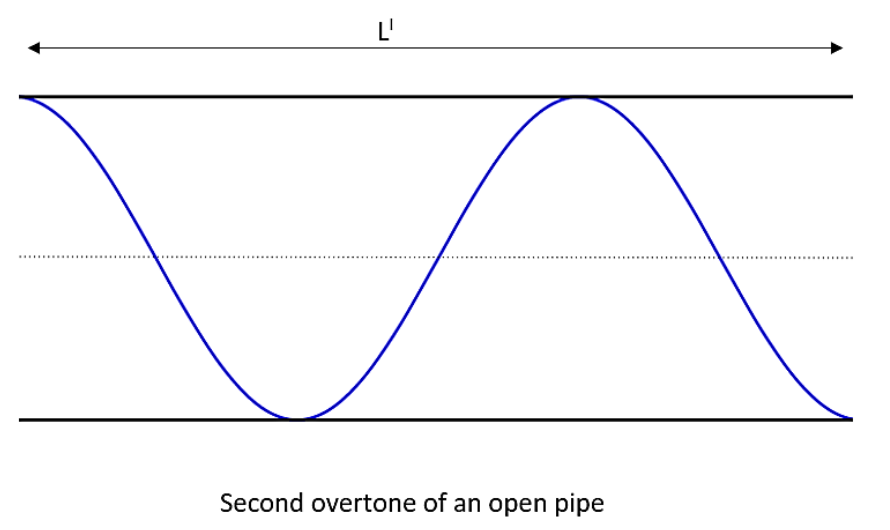
It has been assumed that the second overtone of an open pipe is having the similar frequency as the first overtone of a closed pipe $2m$ long. The length of the open pipe will be
$\begin{aligned} & A.8m \\\ & B.4m \\\ & C.2m \\\ & D.1m \\\ \end{aligned}$

Answer 1

The first overtone frequency of the closed pipe is to be found at first. And then the second overtone frequency of an open pipe is to be found. These values will be equal. Therefore compare these values and reach the final solution needed.

Complete step-by-step solution
__
__
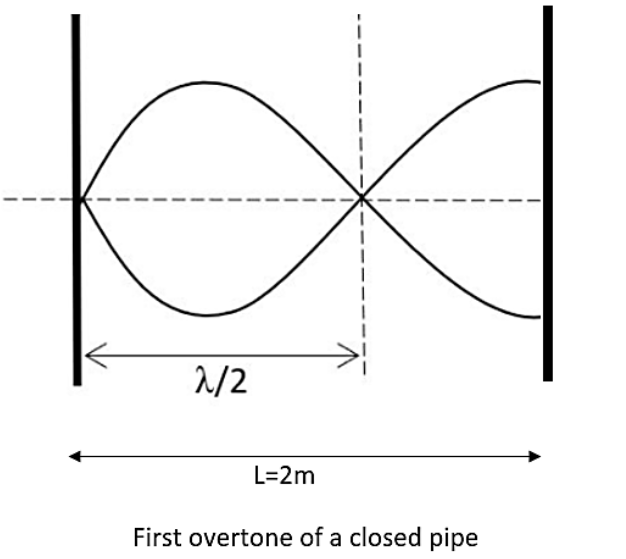
The frequency of the first overtone of a close pipe should be calculated first. The general equation of the frequency of the closed pipe is given as,
${{f}_{2n-1}}=\dfrac{\left( 2n-1 \right)v}{4L}$
Where $n$ be the harmonics, $v$ be the velocity and $L$ be the length of the pipe. One overtone will be the $n-1$ of the harmonics. Which means if it is the first overtone, then it will be twice the fundamental frequency. The first overtone is the second harmonic of the closed pipe. Therefore here the value can be given as,
$n=2$
Substituting this in the equation will give,
${{f}_{3}}^{\prime }=\dfrac{\left( 2\times 2-1 \right)v}{4L}=\dfrac{3v}{4L}$
The general equation of the frequency in an open pipe can be written as,
${{f}_{n}}=\dfrac{nv}{2{L}'}$
As it is the second overtone in an open pipe, the value of $n$ will be given as,
$n=3$
And ${L}'$ be the length of the open pipe.
Substituting the values in the equation will give,
${{f}_{3}}=\dfrac{3v}{2{L}'}$
As these value of frequencies are equal as mentioned in the question, we can write that,
${{f}_{3}}^{\prime }={{f}_{3}}$
That is,
$\dfrac{3v}{2{L}'}=\dfrac{3v}{4L}$
From this equation, after the simplifications, we can write that,
${L}'=2L$
It has been given in the question that the value of the length of the closed pipe is,
$L=2m$
Therefore, the length of the open pipe will be given as,
${L}'=2\times 2=4m$
Answer has been mentioned as option B.

Note: Overtone is a term defined as the frequency of the standing wave at any higher-frequency. Whereas the term harmonic is applicable for those cases in which the frequencies of the overtones are given as the integral multiples of the frequency of the fundamental. Overtones or harmonics are also known as resonances.