Question
Question: Ion the arrangement as shown below, \({{m}_{1}}=1kg\), \({{m}_{2}}=2kg\). Pulleys are massless and s...
Ion the arrangement as shown below, m1=1kg, m2=2kg. Pulleys are massless and strings are light. For what value of M, the mass m1 will move with constant velocity? (Neglect friction)
(1). 4kg
(2). 8kg
(3). 6kg
(4). 10kg
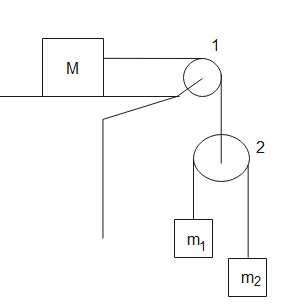
Solution
The system of blocks and pulleys is isolated as no external forces are acting on it. All the forces acting between the elements of the system are internal forces. We can resolve forces along the different directions and use it to make equations. Using the equations, we can calculate the required parameter.
Formula Used:
m1g=T
m2g−T=m2a
2T=Ma1
Complete step-by-step solution:
Given a system of three blocks attached to two pulleys, mass m1 is moving with constant velocity, this means net forces acting on it are zero.
The forces acting on the system are as shown,
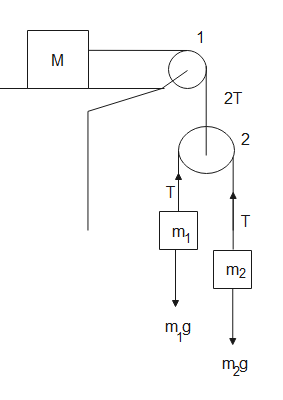
Forces acting on m1 are-
m1g=T
From the above equation, we get,
T=1×g∴T=g
The forces acting on m2 are
m2g−T=m2a
When we substitute given values in the above equation, we get,
2×g−g=2×a⇒g=2a∴a=2g
m2 is moving with acceleration, 2g.
Let the mass M move with acceleration, a1 . so the whole system will move with acceleration a1. The forces acting on the string will cause it to stretch, since there is no movement on the string, the accelerations cancel each other.
a−a1−a1=0⇒a=2a1⇒a1=2a∴a1=2g
The forces acting on mass M are-
2T=Ma1⇒a12T=M⇒2g2×g=M∴4kg=M
Therefore, the mass of M for which m1 moves with constant velocity is 4kg.
Hence, the correct option is (1).
Note:
The tension in a string is the pulling force acting on a string. It is the action-reaction pair of forces acting on the point at which a string is connected to an object. The pulleys and strings are considered massless. The action-reaction pairs follow Newton’s third law of motion, which states that forces acting between two bodies are equal and opposite. According to Newton’s second law of motion, a force is required to change the state of rest or motion of an object.
