Question

$\int(x^6+x^3)\sqrt[3]{x^3+2}dx$

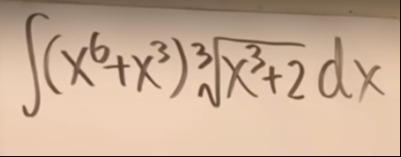
Answer 1

$\frac{1}{8}\,x^4\,(x^3+2)^{4/3}+C.$

Answer 2

We start with the integral

$$I=\int (x^6+x^3)\sqrt[3]{x^3+2}\,dx.$$

Notice that

$$x^6+x^3=x^3(x^3+1).$$

We guess an antiderivative of the form

$$F(x)=\frac{1}{8}\,x^4\,(x^3+2)^{4/3}.$$

Differentiate $F(x)$:

$$\begin{aligned} F'(x) &=\frac{1}{8}\left[4x^3\,(x^3+2)^{4/3}+x^4\cdot\frac{4}{3}\,(x^3+2)^{1/3}\cdot 3x^2\right]\\[1mm] &=\frac{1}{8}\left[4x^3\,(x^3+2)^{4/3}+4x^6\,(x^3+2)^{1/3}\right]\\[1mm] &=\frac{1}{2}\left[x^3\,(x^3+2)^{4/3}+x^6\,(x^3+2)^{1/3}\right]. \end{aligned}$$

Factor out $x^3\,(x^3+2)^{1/3}$:

$$F'(x)=\frac{1}{2}\,x^3\,(x^3+2)^{1/3}\Big[(x^3+2)+x^3\Big] =\frac{1}{2}\,x^3\,(x^3+2)^{1/3}\,(2x^3+2).$$

Since $2x^3+2=2(x^3+1)$, we have

$$F'(x)= x^3\,(x^3+2)^{1/3}(x^3+1),$$

which is exactly the given integrand.

Thus, the antiderivative is

$$\frac{1}{8}\,x^4\,(x^3+2)^{4/3}+C.$$