Question
Question: $\int\frac{x^2 + cos^2x}{(1+x^2)sin^2x}dx$ is equals to...
∫(1+x2)sin2xx2+cos2xdx is equals to
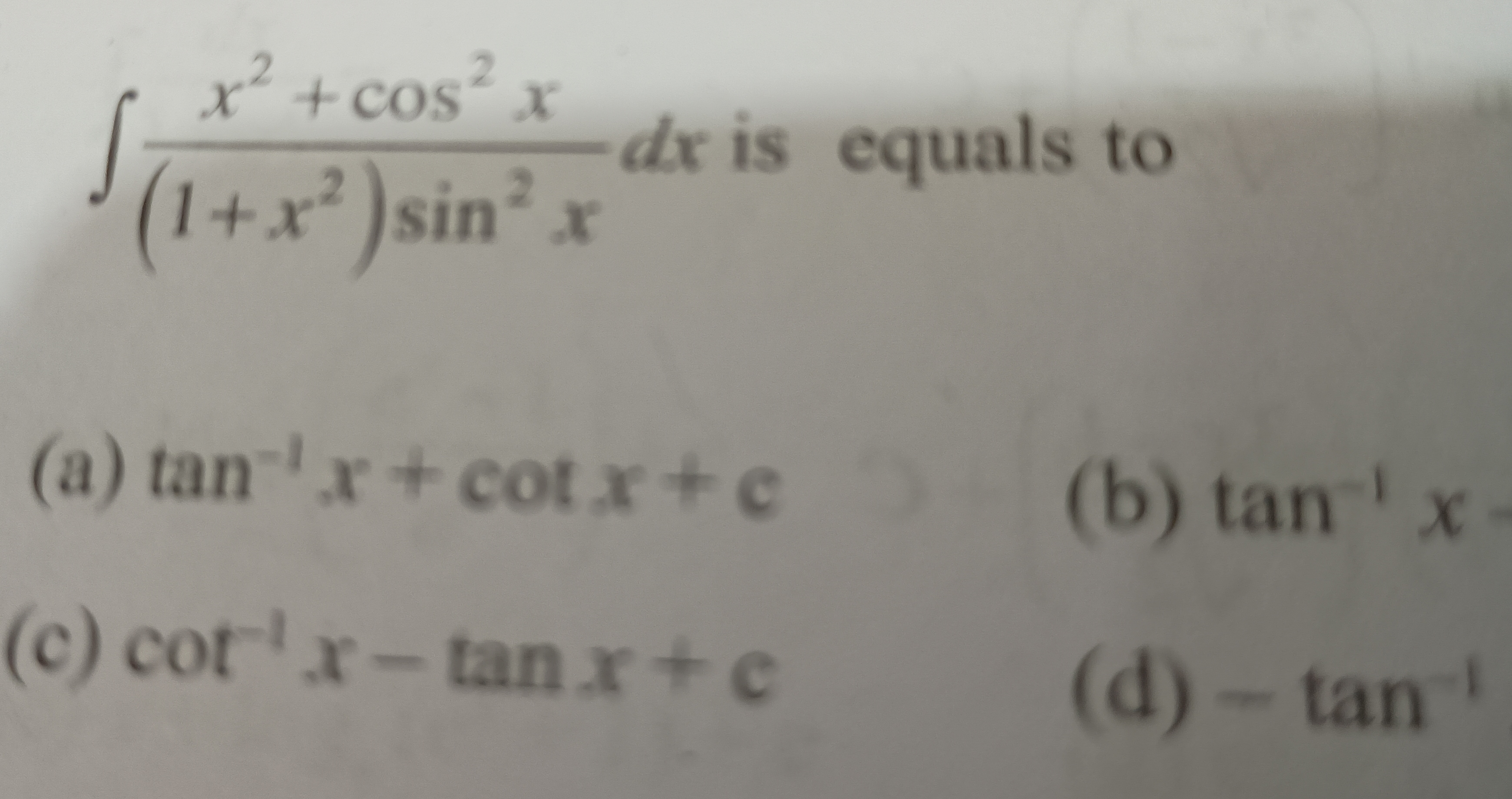
tan−1x+cotx+c
tan−1x
cot−1x−tanx+c
−tan−1
tan−1x+cotx+c
Solution
The given integral is: I=∫(1+x2)sin2xx2+cos2xdx
Step 1: Rewrite the numerator. We know the identity cos2x=1−sin2x. Substitute this into the numerator: x2+cos2x=x2+(1−sin2x)=(x2+1)−sin2x
Step 2: Substitute the rewritten numerator into the integral. I=∫(1+x2)sin2x(x2+1)−sin2xdx
Step 3: Split the integrand into two separate fractions. I=∫((1+x2)sin2xx2+1−(1+x2)sin2xsin2x)dx
Step 4: Simplify each term. The first term simplifies by canceling (x2+1): (1+x2)sin2xx2+1=sin2x1 The second term simplifies by canceling sin2x: (1+x2)sin2xsin2x=1+x21 So the integral becomes: I=∫(sin2x1−1+x21)dx
Step 5: Use trigonometric identity for the first term. Recall that sin2x1=csc2x. I=∫(csc2x−1+x21)dx
Step 6: Integrate term by term. The standard integral of csc2x is −cotx. The standard integral of 1+x21 is tan−1x. Therefore, I=−cotx−tan−1x+C
Step 7: Compare the result with the given options. Our calculated result is −cotx−tan−1x+C. Let's check the options: (a) tan−1x+cotx+c (b) tan−1x (c) cot−1x−tanx+c (d) −tan−1x
Our result is −(tan−1x+cotx)+C. Option (a) is (tan−1x+cotx)+C. There is a sign difference between our derived answer and option (a). However, option (a) contains the correct functional forms (tan−1x and cotx). Given that this is a multiple-choice question and option (a) is the only one with these correct functions, it is highly probable that there is a sign error in the question or the option itself. If we were to differentiate option (a), we would get the negative of the original integrand. dxd(tan−1x+cotx+C)=1+x21−csc2x=1+x21−sin2x1=(1+x2)sin2xsin2x−(1+x2)=(1+x2)sin2xsin2x−1−x2=(1+x2)sin2x−cos2x−x2=−(1+x2)sin2xx2+cos2x Since the derivative of option (a) is the negative of the integrand, the integral of the given expression would be the negative of option (a). However, among the given choices, option (a) is the most appropriate if we assume a sign error in the question or options.
