Question

Intercept made by the circle${x^2} + {y^2} - 5x - 13y - 14 = 0$ on the x-axis and y-axis respectively {\text{A}}{\text{. 9,13}} \\\ {\text{B}}{\text{. 5,13}} \\\ {\text{C}}{\text{. 9,15}} \\\ {\text{D}}{\text{. None of these}} \\\

Answer 1

Hint:- The x-intercepts are where the graph crosses the x-axis, and the y-intercepts are where the graph crosses the y-axis. Algebraically, an x-intercept is a point on the graph where y is zero, and a y-intercept is a point on the graph where x is zero.

Complete step-by-step solution -
Length of intercept on x-axis =|difference between roots of equation in which y=0 |Length of intercept on y-axis = |difference between roots of equation in which x=0 |.

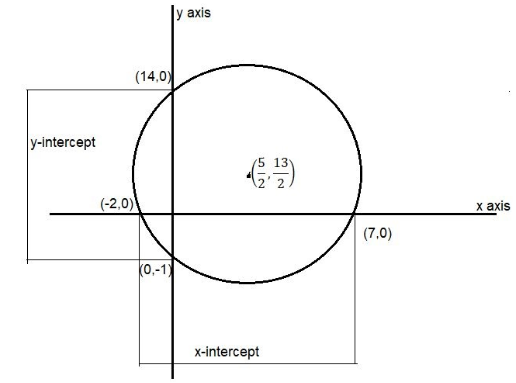
Given
Equation of circle ${x^2} + {y^2} - 5x - 13y - 14 = 0$ eq 1.
Now to find the intercept on x-axis we have to put y=0 in eq 1.
$\Rightarrow$ ${x^2} - 5x - 14 = 0$ eq 2.
Above equation is a quadratic equation it means given circle intersect x-axis at two points
On solving eq 2.
$\Rightarrow$ $\left( {x - 7} \right)(x + 2) = 0$
$\Rightarrow$ $x$ = 7 , -2
Hence intercepts on the x-axis by the given circle are 7, -2.
Now, the length of intercept on x-axis = |difference between roots of equation in which y=0 |
$= |7 - ( - 2)| \\\ = 9 \\\$
Now to find the intercept on the y-axis we have to put x=0 in eq 1.
$\Rightarrow$ ${y^2} - 13y - 14 = 0$ eq 3.
Above equation is a quadratic equation it means given circle intersect y-axis at two points
On solving eq 3.
$\Rightarrow$ $(y - 14)(y + 1) = 0$
$\Rightarrow$ y = 14 , -1
Hence intercepts on the y-axis by the given circle are 14, -1.
Now, the length of intercept on y-axis = |difference between roots of equation in which x=0 |
$= |14 - ( - 1)| \\\ = 15 \\\$
Hence, intercepts on x-axis and y-axis by circle ${x^2} + {y^2} - 5x - 13y - 14 = 0$ are respectively 9,15.
Option C is correct.

Note: -Whenever you get this type of question the key concept of solving is if you have to put y=0 for x intercept in given equation of circle and for y intercept you have to put x=0 in equation of circle and then take absolute difference between the roots of equation in which are the intercepts of circle on both axis. Or you can use direct formula of length of intercept on both axis by circle for general equation of circle${x^2} + {y^2} + 2gx + 2fy + c = 0$
length of intercept on $x -$axis =$2 \sqrt {{g^2} - c}$
length of intercept on $y -$axis =$2 \sqrt {{f^2} - c}$