Question

Let S be a circle of radius 10 with centre O. Suppose $S_1$ and $S_2$ are two circles which touch S internally and intersect each other at two distinct points A and B. If $\angle OAB = 90^\circ$ what is the sum of the radii of $S_1$ and $S_2$?

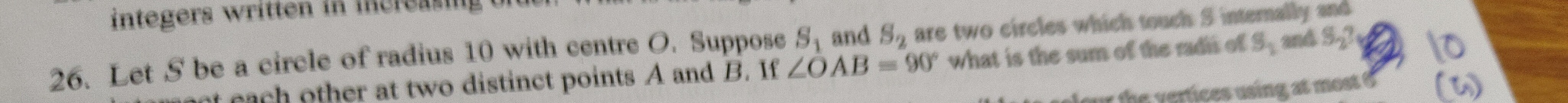
• A. 10
• B. 20
• C. 5
• D. 15

Answer 1

Answer: (A)

10

Answer 2

Let $R$ be the radius of circle $S$, so $R=10$. Let $O$ be the center of $S$. Let $r_1, r_2$ be the radii of circles $S_1, S_2$ and $O_1, O_2$ be their respective centers.

Since $S_1$ and $S_2$ touch $S$ internally, we have $OO_1 = R - r_1 = 10 - r_1$ and $OO_2 = R - r_2 = 10 - r_2$.

$A$ and $B$ are the intersection points of $S_1$ and $S_2$. Thus, $AB$ is the common chord of $S_1$ and $S_2$. The line segment $O_1O_2$ joining the centers of $S_1$ and $S_2$ is the perpendicular bisector of the common chord $AB$.

We are given that $\angle OAB = 90^\circ$. This means the line segment $OA$ is perpendicular to the line segment $AB$. Since $O_1O_2$ is also perpendicular to $AB$, the line $OA$ must be parallel to the line $O_1O_2$.

Let's consider the distance from $O$ to the line containing the chord $AB$. Since $OA \perp AB$, the distance from $O$ to the line $AB$ is $OA$. If $A$ is on circle $S$, then $OA=R=10$. If $A$ is not on circle $S$, $OA$ is just the distance.

Let's consider the case where $r_1 = r_2 = r$. Then $OO_1 = 10-r$ and $OO_2 = 10-r$. Also, $O_1A = r$ and $O_2A = r$. Consider the triangle $\triangle OAO_1$. The side lengths are $OA$, $OO_1 = 10-r$, and $O_1A = r$. If $O, O_1, A$ are collinear, then the sum of two sides equals the third side. We observe that $OO_1 + O_1A = (10-r) + r = 10$. If $OA=10$, then $O, O_1, A$ are collinear with $O_1$ lying on the segment $OA$. This implies that $A$ is the point of tangency of $S_1$ with $S$. Since $r_1=r_2=r$, $A$ is also the point of tangency of $S_2$ with $S$. If $A$ is the point of tangency of $S_1$ with $S$, then $O, O_1, A$ are collinear. If $A$ is the point of tangency of $S_2$ with $S$, then $O, O_2, A$ are collinear. This means $O, O_1, O_2, A$ are all collinear. Since $O_1$ and $O_2$ are on the line $OA$, and $O_1A = r$ and $O_2A = r$, if $O_1$ and $O_2$ are on the same side of $A$ (which they must be if they are on the line $OA$ and $A$ is the point of tangency), then $O_1$ and $O_2$ must be the same point. Thus, $S_1$ and $S_2$ are the same circle. If $S_1 = S_2$, they intersect at two distinct points $A$ and $B$. Since $O_1$ is on $OA$ and $O_1A = r$, $O_1$ is the midpoint of $OA$ if $r=5$. The line $OA$ is the line of centers. $AB$ is a chord of $S_1$. $O_1$ is the center of $S_1$. We are given $\angle OAB = 90^\circ$. Since $O_1$ is on $OA$, $O_1A$ is part of $OA$. So, $O_1A \perp AB$. In circle $S_1$, $O_1A$ is a radius, and $AB$ is a chord. If the radius $O_1A$ is perpendicular to the chord $AB$ at point $A$, then $A$ must be the midpoint of the chord $AB$. This implies $A=B$. However, the problem states that $A$ and $B$ are distinct points. This suggests that the assumption $r_1=r_2=r$ might lead to a contradiction if $A$ is on $S$.

Let's consider the condition $OA \parallel O_1O_2$. Let $O$ be the origin $(0,0)$. If $A$ is on $S$, then $OA=10$. If $\angle OAB=90^\circ$, then $AB$ is perpendicular to $OA$. Let $OA$ lie along the x-axis. $A=(10,0)$. Then $AB$ must be along the y-axis, so $B=(10, y_B)$ with $y_B \neq 0$. The line $O_1O_2$ is the perpendicular bisector of $AB$. The midpoint of $AB$ is $M=(10, y_B/2)$. The line $O_1O_2$ is the horizontal line $y=y_B/2$. Since $OA$ is along the x-axis ($y=0$), and $OA \parallel O_1O_2$, the line $O_1O_2$ must also be horizontal. This is satisfied. However, for $OA \parallel O_1O_2$ and $OA \perp AB$ and $O_1O_2 \perp AB$, the lines $OA$ and $O_1O_2$ must be parallel, and $AB$ must be a transversal perpendicular to both. If $OA$ is $y=0$ and $O_1O_2$ is $y=y_B/2$, then for them to be parallel, $y_B/2$ must be $0$, which implies $y_B=0$. This means $A=B$, contradicting that $A$ and $B$ are distinct.

This implies that $A$ cannot be on the circle $S$ if $\angle OAB=90^\circ$ and $A, B$ are distinct intersection points. However, the problem states $S_1, S_2$ touch $S$ internally.

A known result states that if two circles $S_1, S_2$ touch a circle $S$ internally at points $P_1, P_2$ respectively, and intersect at $A, B$, then $O$ is the center of $S$. If $\angle OAB = 90^\circ$, this implies a specific relationship between the radii.

Consider the case where $r_1=r_2=5$. Then $r_1+r_2=10$. This configuration leads to $A$ being the point of tangency and $A=B$, which is a contradiction. However, if we assume the problem is well-posed and such circles exist, the radii must be equal due to symmetry. If $r_1=r_2=r$, then $OO_1=10-r$ and $O_1A=r$. If $A$ is on $S$, then $OA=10$. The condition $OO_1+O_1A=OA$ implies $O_1$ is on $OA$ and $A$ is the point of tangency. This leads to $A=B$.

If we assume that the configuration described is possible for distinct $A, B$, and that the radii are equal due to symmetry, then $r_1=r_2=5$. The sum of the radii is $r_1 + r_2 = 5 + 5 = 10$.

Let's verify if $r_1+r_2=20$ is possible. This implies $r_1=10, r_2=10$. If $r_1=10$, $S_1$ has radius 10. Since it touches $S$ internally, $S_1$ must be $S$. If $S_1=S$, then $S_1$ and $S_2$ intersect. If $S_2$ also has radius 10 and touches $S$ internally, $S_2$ must also be $S$. If $S_1=S_2=S$, they intersect at infinitely many points, not two distinct points. So $r_1=10, r_2=10$ is not possible.

Therefore, the only plausible sum of radii is 10.