Question

$\int_{\pi}^{2\pi}[4\sin x]dx =$

Answer 1

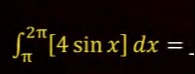
2\arcsin(1/4) + 2\arcsin(3/4) - \frac{11\pi}{3}

Answer 2

To evaluate the integral $\int_{\pi}^{2\pi}[4\sin x]dx$, we first determine the behavior of the function $[4\sin x]$ in the interval $[\pi, 2\pi]$.

In the interval $[\pi, 2\pi]$, $\sin x$ ranges from $0$ down to $-1$ and back to $0$. Thus, $4\sin x$ ranges from $0$ down to $-4$ and back to $0$. The possible integer values for $[4\sin x]$ are $-1, -2, -3, -4$.

The value of $[4\sin x]$ changes when $4\sin x$ crosses an integer. We find the $x$ values in $[\pi, 2\pi]$ where $4\sin x$ equals $-1, -2, -3, -4$: \begin{itemize} \item $4\sin x = -1 \implies \sin x = -1/4$. Let $\alpha_1 = \arcsin(1/4)$. In $[\pi, 2\pi]$, this occurs at $x = \pi + \alpha_1$ and $x = 2\pi - \alpha_1$. \item $4\sin x = -2 \implies \sin x = -1/2$. In $[\pi, 2\pi]$, this occurs at $x = \pi + \pi/6 = 7\pi/6$ and $x = 2\pi - \pi/6 = 11\pi/6$. \item $4\sin x = -3 \implies \sin x = -3/4$. Let $\alpha_3 = \arcsin(3/4)$. In $[\pi, 2\pi]$, this occurs at $x = \pi + \alpha_3$ and $x = 2\pi - \alpha_3$. \item $4\sin x = -4 \implies \sin x = -1$. In $[\pi, 2\pi]$, this occurs at $x = 3\pi/2$. \end{itemize} The ordered critical points in $[\pi, 2\pi]$ are: $\pi, \pi+\alpha_1, 7\pi/6, \pi+\alpha_3, 3\pi/2, 2\pi-\alpha_3, 11\pi/6, 2\pi-\alpha_1, 2\pi$.

We can calculate the integral by summing the product of the constant value of $[4\sin x]$ in each sub-interval and the length of that sub-interval. Alternatively, we can sum the product of each integer value $k$ and the total length of the set $\{x \in [\pi, 2\pi] : [4\sin x] = k\}$.

\begin{itemize} \item For $[4\sin x] = -1$: The set is $(\pi, \pi+\alpha_1) \cup (2\pi-\alpha_1, 2\pi)$. The total length is $\alpha_1 + \alpha_1 = 2\alpha_1$. Contribution: $(-1)(2\alpha_1) = -2\alpha_1$. \item For $[4\sin x] = -2$: The set is $(\pi+\alpha_1, 7\pi/6) \cup (11\pi/6, 2\pi-\alpha_1)$. The total length is $(7\pi/6 - (\pi+\alpha_1)) + (2\pi-\alpha_1 - 11\pi/6) = (\pi/6 - \alpha_1) + (\pi/6 - \alpha_1) = \pi/3 - 2\alpha_1$. Contribution: $(-2)(\pi/3 - 2\alpha_1) = -2\pi/3 + 4\alpha_1$. \item For $[4\sin x] = -3$: The set is $(7\pi/6, \pi+\alpha_3) \cup (2\pi-\alpha_3, 11\pi/6)$. The total length is $(\pi+\alpha_3 - 7\pi/6) + (11\pi/6 - (2\pi-\alpha_3)) = (\alpha_3 - \pi/6) + (\alpha_3 - \pi/6) = 2\alpha_3 - \pi/3$. Contribution: $(-3)(2\alpha_3 - \pi/3) = -6\alpha_3 + \pi$. \item For $[4\sin x] = -4$: The set is $(\pi+\alpha_3, 3\pi/2) \cup (3\pi/2, 2\pi-\alpha_3)$. The total length is $(3\pi/2 - (\pi+\alpha_3)) + (2\pi-\alpha_3 - 3\pi/2) = (\pi/2 - \alpha_3) + (\pi/2 - \alpha_3) = \pi - 2\alpha_3$. Contribution: $(-4)(\pi - 2\alpha_3) = -4\pi + 8\alpha_3$. \end{itemize} Summing the contributions: $(-2\alpha_1) + (-2\pi/3 + 4\alpha_1) + (-6\alpha_3 + \pi) + (-4\pi + 8\alpha_3)$ $= (-2\alpha_1 + 4\alpha_1) + (-6\alpha_3 + 8\alpha_3) + (-2\pi/3 + \pi - 4\pi)$ $= 2\alpha_1 + 2\alpha_3 - 2\pi/3 - 3\pi$ $= 2\alpha_1 + 2\alpha_3 - 2\pi/3 - 9\pi/3$ $= 2\alpha_1 + 2\alpha_3 - \frac{11\pi}{3}$ Substituting $\alpha_1 = \arcsin(1/4)$ and $\alpha_3 = \arcsin(3/4)$, the integral is $2\arcsin(1/4) + 2\arcsin(3/4) - \frac{11\pi}{3}$.