Question

$\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}} \frac{dx}{1 + \cos x}$ is equal to

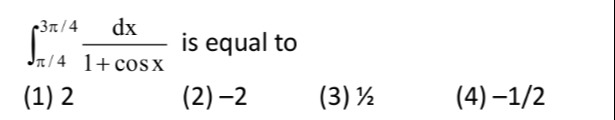
• A. 2
• B. -2
• C. ½
• D. -1/2

Answer 1

Answer: (A)

2

Answer 2

Step 1: Use the identity

$$1 + \cos x = 2\cos^2\!\bigl(\tfrac{x}{2}\bigr)$$

Hence

$$\frac{1}{1 + \cos x} = \frac{1}{2\cos^2\!\bigl(\tfrac{x}{2}\bigr)} = \tfrac12\,\sec^2\!\bigl(\tfrac{x}{2}\bigr).$$

Step 2: Integrate

$$\int \frac{dx}{1 + \cos x} = \tfrac12 \int \sec^2\!\bigl(\tfrac{x}{2}\bigr)\,dx = \tfrac12 \cdot 2\,\tan\!\bigl(\tfrac{x}{2}\bigr) = \tan\!\bigl(\tfrac{x}{2}\bigr).$$

Step 3: Evaluate definite integral

$$\left.\tan\!\bigl(\tfrac{x}{2}\bigr)\right|_{\pi/4}^{3\pi/4} = \tan\!\bigl(\tfrac{3\pi}{8}\bigr) - \tan\!\bigl(\tfrac{\pi}{8}\bigr).$$

Using

$$\tan\!\bigl(\tfrac{3\pi}{8}\bigr)=1+\sqrt2,\quad \tan\!\bigl(\tfrac{\pi}{8}\bigr)=\sqrt2-1,$$

we get

$$(1+\sqrt2)-(\sqrt2-1)=2.$$