Solveeit Logo
Login

Question

Question: \(\int_{}^{}{e^{x}\frac{(1 + nx^{n–1}–x^{2n})}{(1–x^{n})\sqrt{1–x^{2n}}}}\) dx =...

∫ex(1+nxn–1–x2n)(1–xn)1–x2n\int_{}^{}{e^{x}\frac{(1 + nx^{n–1}–x^{2n})}{(1–x^{n})\sqrt{1–x^{2n}}}} dx =

A

ex1–xn1+xn\sqrt{\frac{1–x^{n}}{1 + x^{n}}} + c

B

ex1+xn1–xn\sqrt{\frac{1 + x^{n}}{1–x^{n}}}+ c

C

– ex1–xn1+xn\sqrt{\frac{1–x^{n}}{1 + x^{n}}} + c

D

– ex1+xn1–xn\sqrt{\frac{1 + x^{n}}{1–x^{n}}} + c

Answer

ex1+xn1–xn\sqrt{\frac{1 + x^{n}}{1–x^{n}}}+ c

Explanation

Solution

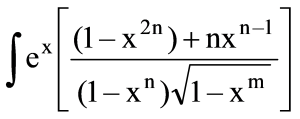
dx f(x) = 1+xn1–xn\sqrt{\frac{1 + x^{n}}{1–x^{n}}}

f ' (x) = nxn–1(1–xn)1–x2n\frac{nx^{n–1}}{(1–x^{n})\sqrt{1–x^{2n}}}

\ ̃ ex 1+xn1–xn\sqrt{\frac{1 + x^{n}}{1–x^{n}}}+ c