Question
Question: $\int_1^0 ((1-x^{25})\frac{20}{1} - (1-x^{20})\frac{25}{1}) dx$ (VII)...
∫10((1−x25)120−(1−x20)125)dx (VII)
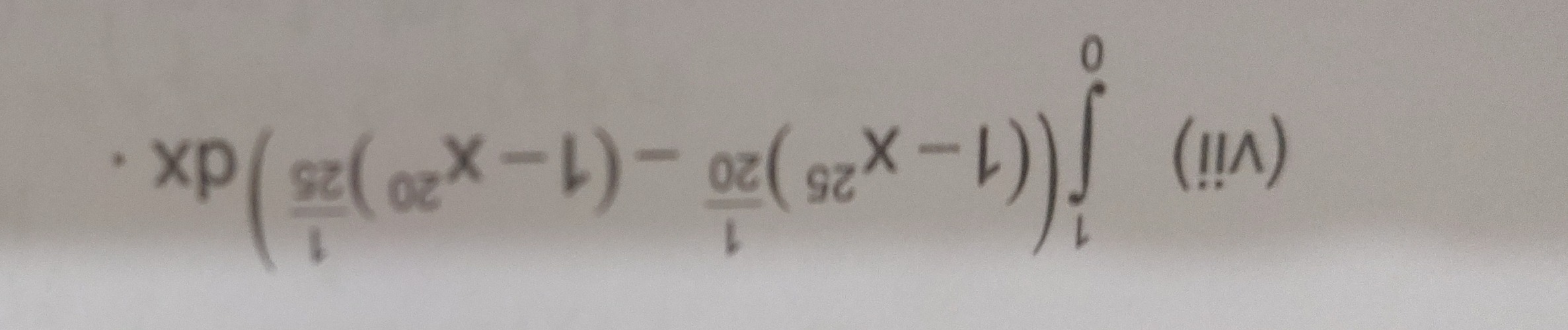
2731250
Solution
The problem asks us to evaluate the definite integral ∫10((1−x25)120−(1−x20)125)dx.
First, simplify the integrand: (1−x25)20−(1−x20)25 =20−20x25−(25−25x20) =20−20x25−25+25x20 =25x20−20x25−5
Now, substitute this simplified expression back into the integral: I=∫10(25x20−20x25−5)dx
We can integrate term by term using the power rule for integration, ∫xndx=n+1xn+1: ∫(25x20−20x25−5)dx=2520+1x20+1−2025+1x25+1−5x =2521x21−2026x26−5x =2125x21−1310x26−5x
Now, evaluate the definite integral using the limits from 1 to 0: I=[2125x21−1310x26−5x]10 Apply the Fundamental Theorem of Calculus, which states ∫abf(x)dx=F(b)−F(a): I=(2125(0)21−1310(0)26−5(0))−(2125(1)21−1310(1)26−5(1)) I=(0−0−0)−(2125−1310−5) I=−(2125−1310−5) I=−2125+1310+5
To combine these fractions, find a common denominator for 21 and 13. Since 21 and 13 are coprime, the least common multiple (LCM) is 21×13=273. I=21×13−25×13+13×2110×21+2735×273 I=273−325+273210+2731365 I=273−325+210+1365 I=273−115+1365 I=2731250
