Question

$\int_{0}^{v}\frac{dv}{F-rv} = \int_{0}^{t}\frac{dt}{M+rt}$

Answer 1

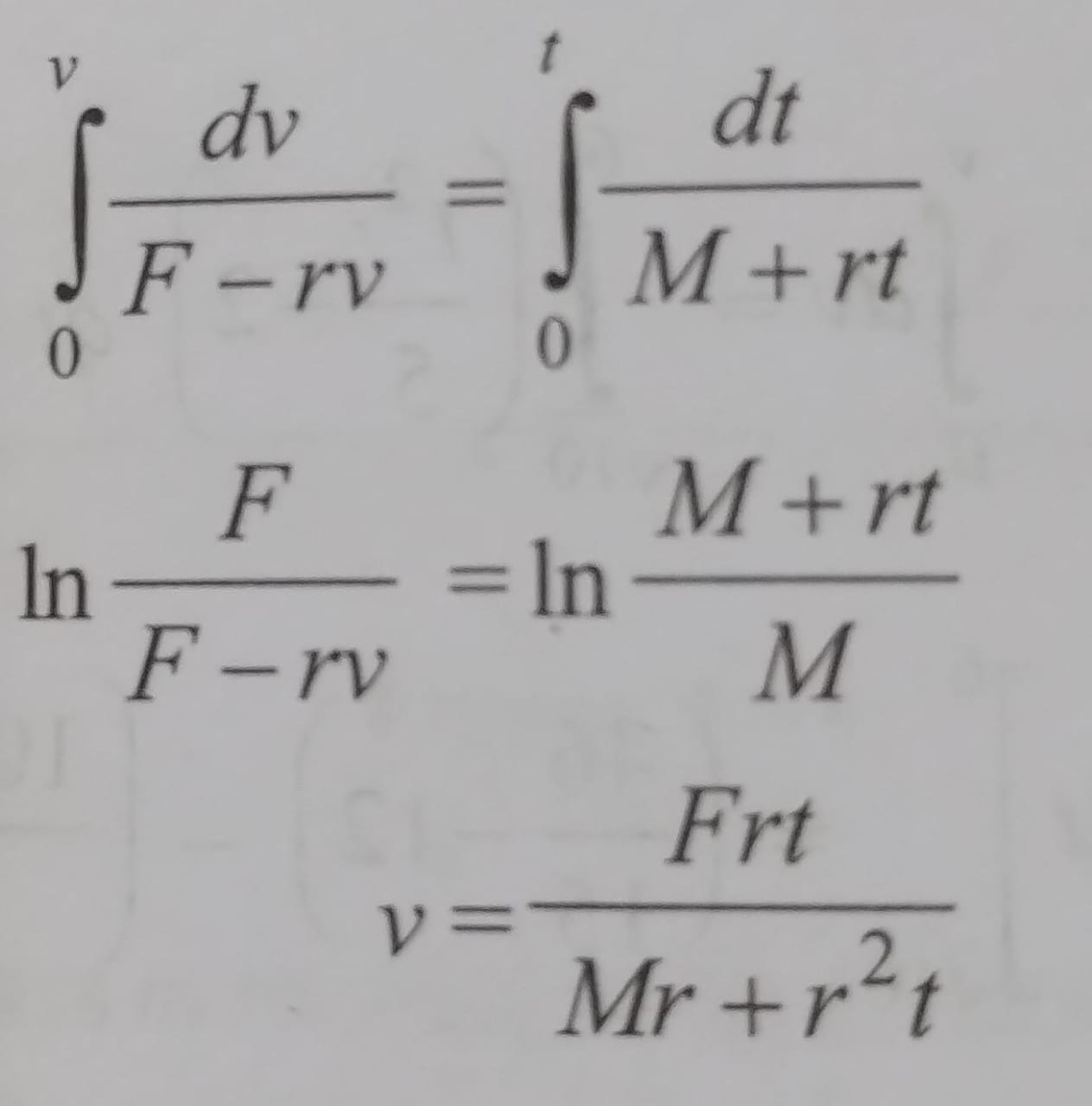
The final expression for $v$ is: $v = \frac{Frt}{rM + r^2t}$

Answer 2

The problem provides a derivation starting from an integral equation and ending with an expression for $v$. The task is to present the solution, which involves verifying and explaining these steps.

The given integral equation is: $\int_{0}^{v}\frac{dv}{F-rv} = \int_{0}^{t}\frac{dt}{M+rt}$

Explanation of the Solution

1. Integrate the Left-Hand Side (LHS): Let $u = F-rv$. Then, $du = -r \, dv$, which implies $dv = -\frac{1}{r} du$. The limits of integration change: when $v=0$, $u=F$; when $v=v$, $u=F-rv$. $\text{LHS} = \int_{F}^{F-rv} \frac{1}{u} \left(-\frac{1}{r}\right) du = -\frac{1}{r} [\ln|u|]_{F}^{F-rv}$ $= -\frac{1}{r} (\ln|F-rv| - \ln|F|) = \frac{1}{r} (\ln|F| - \ln|F-rv|)$ Assuming $F > 0$ and $F-rv > 0$ (typical for physical scenarios where $v$ is less than terminal velocity): $\text{LHS} = \frac{1}{r} \ln\left(\frac{F}{F-rv}\right)$

2. Integrate the Right-Hand Side (RHS): Let $w = M+rt$. Then, $dw = r \, dt$, which implies $dt = \frac{1}{r} dw$. The limits of integration change: when $t=0$, $w=M$; when $t=t$, $w=M+rt$. $\text{RHS} = \int_{M}^{M+rt} \frac{1}{w} \left(\frac{1}{r}\right) dw = \frac{1}{r} [\ln|w|]_{M}^{M+rt}$ $= \frac{1}{r} (\ln|M+rt| - \ln|M|)$ Assuming $M > 0$ and $M+rt > 0$ (which is true for positive mass and time): $\text{RHS} = \frac{1}{r} \ln\left(\frac{M+rt}{M}\right)$

3. Equate and Simplify: Equating the integrated LHS and RHS: $\frac{1}{r} \ln\left(\frac{F}{F-rv}\right) = \frac{1}{r} \ln\left(\frac{M+rt}{M}\right)$ Multiplying both sides by $r$: $\ln\left(\frac{F}{F-rv}\right) = \ln\left(\frac{M+rt}{M}\right)$ This matches the second line of the provided derivation.

4. Solve for $v$: Exponentiate both sides (take $e$ to the power of both sides) to remove the logarithms: $e^{\ln\left(\frac{F}{F-rv}\right)} = e^{\ln\left(\frac{M+rt}{M}\right)}$ $\frac{F}{F-rv} = \frac{M+rt}{M}$ Cross-multiply: $F \cdot M = (F-rv)(M+rt)$ Expand the right side: $FM = FM + Frt - rvM - r^2vt$ Subtract $FM$ from both sides: $0 = Frt - rvM - r^2vt$ Rearrange the terms to solve for $v$: $rvM + r^2vt = Frt$ Factor out $v$ from the terms on the left: $v(rM + r^2t) = Frt$ Finally, solve for $v$: $v = \frac{Frt}{rM + r^2t}$ This matches the third line of the provided derivation.