Question

$\int_{0}^{v} dv = \int_{0}^{t} \frac{Fdt}{m_0 - \mu t}$

$v = \frac{F}{\mu} ln(\frac{m_0}{m_0 - \mu t})$

Answer 1

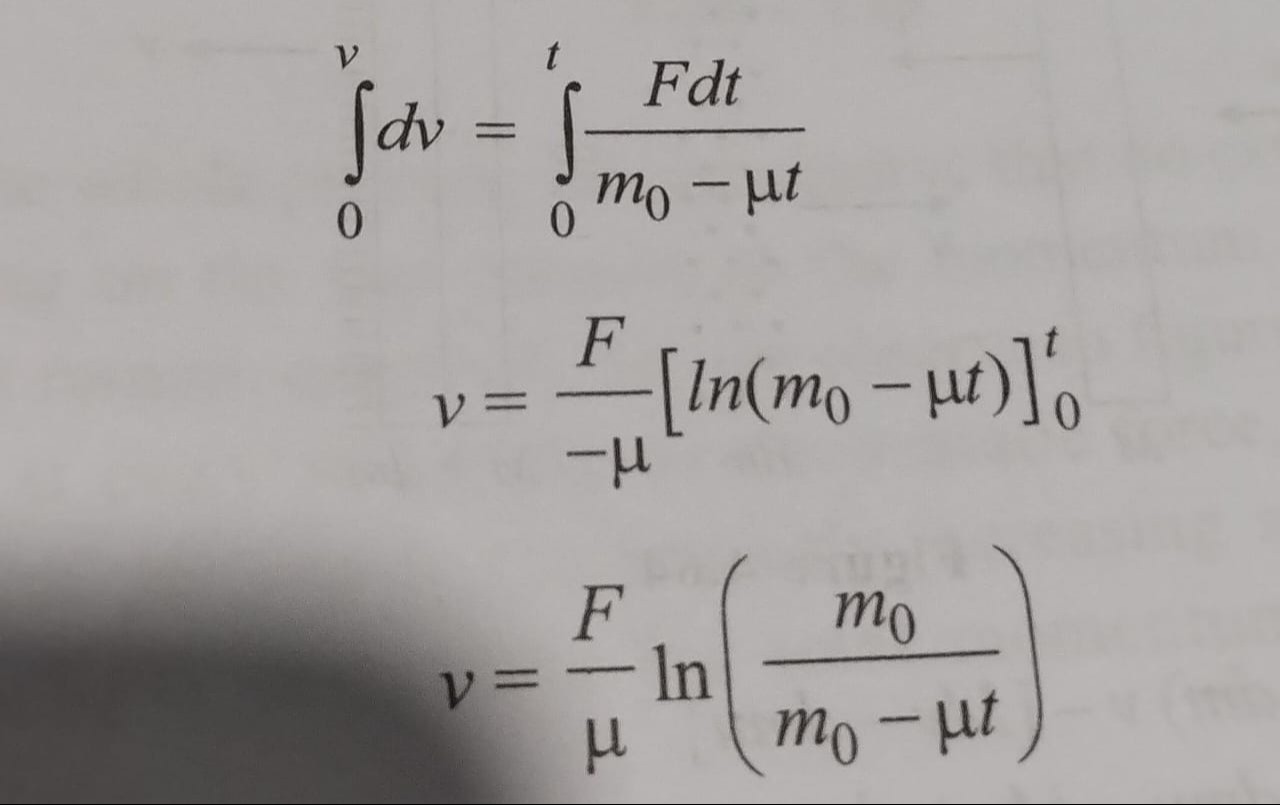
The derived expression for velocity $v$ as a function of time $t$ is: $v = \frac{F}{\mu} \ln\left(\frac{m_0}{m_0 - \mu t}\right)$

Answer 2

The derivation involves setting up the differential equation for velocity $v$ based on Newton's second law for a system with changing mass ($m(t) = m_0 - \mu t$) under a constant force $F$: $(m_0 - \mu t) \frac{dv}{dt} = F$. This is followed by separating variables and integrating both sides from initial conditions ($t=0, v=0$) to general conditions ($t, v$). The integration of $\frac{1}{m_0 - \mu t}$ yields a logarithmic term, which, after applying the limits and simplifying using logarithm properties, gives the final expression for $v$.

The equation of motion for an object with changing mass is generally given by $m(t) \frac{d\vec{v}}{dt} = \vec{F}_{ext} + \vec{v}_{rel} \frac{dm}{dt}$. In this specific problem, the given integral equation suggests a simplified scenario where the net external force is $F$, and the mass changes at a rate $\frac{dm}{dt} = -\mu$. Thus, the instantaneous mass is $m(t) = m_0 - \mu t$. The equation of motion becomes: $(m_0 - \mu t) \frac{dv}{dt} = F$

This can be rewritten as: $\frac{dv}{dt} = \frac{F}{m_0 - \mu t}$

To find the velocity $v$ as a function of time, we integrate this equation. Assuming the object starts from rest ($v=0$ at $t=0$): $\int_{0}^{v} dv = \int_{0}^{t} \frac{F}{m_0 - \mu t} dt$

1. Left-hand side integration: $\int_{0}^{v} dv = [v]_0^v = v - 0 = v$

2. Right-hand side integration: $\int_{0}^{t} \frac{F}{m_0 - \mu t} dt$ Assuming $F$ is a constant, it can be taken out of the integral: $F \int_{0}^{t} \frac{dt}{m_0 - \mu t}$ To solve this integral, we use a substitution. Let $u = m_0 - \mu t$. Then, $du = -\mu dt$, which implies $dt = -\frac{1}{\mu} du$. When $t=0$, $u = m_0 - \mu(0) = m_0$. When $t=t$, $u = m_0 - \mu t$. Substituting these into the integral: $F \int_{m_0}^{m_0 - \mu t} \frac{1}{u} \left(-\frac{1}{\mu} du\right)$ $= -\frac{F}{\mu} \int_{m_0}^{m_0 - \mu t} \frac{1}{u} du$ The integral of $\frac{1}{u}$ is $\ln|u|$. Since $m_0$ and $m_0 - \mu t$ represent mass, they are positive. $= -\frac{F}{\mu} [\ln(u)]_{m_0}^{m_0 - \mu t}$ $= -\frac{F}{\mu} [\ln(m_0 - \mu t) - \ln(m_0)]$ Using the logarithm property $\ln(a) - \ln(b) = \ln(a/b)$: $= -\frac{F}{\mu} \ln\left(\frac{m_0 - \mu t}{m_0}\right)$ Using the logarithm property $-\ln(x) = \ln(1/x)$: $= \frac{F}{\mu} \ln\left(\frac{m_0}{m_0 - \mu t}\right)$

3. Equating both sides: The left side is $v$, and the right side is the result of the integration. $v = \frac{F}{\mu} \ln\left(\frac{m_0}{m_0 - \mu t}\right)$